Cerita Petualangan Fungsi Trigonometri

Bagaimana alur pembelajaran fungsi trigonometri pada mata pelajaran Matematika tingkat lanjut? Artikel ini memberikan penjelasan dan rasional terhadap topik fungsi trigonometri pada fase F+, serta memberikan alternatif alur cerita bagaimana peserta didik berpetualang di dalamnya.

Apa yang perlu dipelajari peserta didik tentang topik trigonometri pada fase F+? Bagaimana memelajarinya? Kedua pertanyaan ini dapat kita jawab dengan melihat kembali modal pengalaman belajar yang telah dimiliki oleh peserta didik. Selain itu, kita juga perlu menganalisis potensi trigonometri dalam membantu peserta didik untuk mendeskripsikan, memprediksi, dan mengomunikasikan fenomena-fenomena di sekitar mereka.

Sebelum masuk ke fase F+, peserta didik paling tidak telah memelajari perbandingan trigonometri untuk segitiga siku-siku. Mereka telah memelajari topik tersebut pada fase E atau kelas 10. Secara khusus, mereka telah mengenal “tiga serangkai” perbandingan trigonometri, yaitu sinus, kosinus, dan tangen, serta menerapkannya untuk menyelesaikan berbagai macam permasalahan. Misalnya, berdasarkan buku Matematika untuk SMA/MA/SMK/MAK Kelas X (Edisi Revisi) peserta didik akan dapat menentukan tinggi Jam Gadang (Bukittinggi, Sumatra Barat) dan lebar Teluk Youtefa yang dilintasi oleh Jembatan Youtefa (Jayapura, Papua) tanpa melakukan pengukuran secara langsung.

Pembelajaran trigonometri apakah hanya cukup sampai perbandingan trigonometri segitiga siku-siku? Mari kita analisis bersama-sama! Perbandingan trigonometri segitiga siku-siku ini memiliki keterbatasan. Perbandingan trigonometri tersebut hanya dapat diterapkan pada permasalahan-permasalahan yang melibatkan sisi-sisi dan sudut-sudut dalam segitiga siku-siku. Padahal, permasalahan-permasalahan yang mungkin dihadapi oleh peserta didik ke depannya:

tidak hanya melibatkan sudut-sudut dalam segitiga siku-siku, yaitu sudut-sudut lancip dan siku-siku; dan
tidak hanya melibatkan kuantitas yang berupa besar sudut tetapi juga berbagai macam kuantitas lainnya, seperti waktu dan jarak.

Dengan alasan seperti itulah mengapa capaian pembelajaran untuk Matematika tingkat lanjut fase F+ memberikan mandat seperti ini.

Peserta didik dapat menyatakan fungsi trigonometri menggunakan lingkaran satuan, memodelkan fenomena periodik dengan fungsi trigonometri, dan membuktikan serta menerapkan identitas trigonometri dan aturan kosinus dan sinus.

Untuk mengilustrasikan pentingnya capaian pembelajaran tersebut, kita dapat memerhatikan fenomena siklus matahari untuk Kota Perth, Australia pada Gambar 1! (Informasi tentang siklus matahari untuk kota-kota lainnya pada periode yang lebih luas dapat dilihat melalui aplikasi kalkulator matahari yang telah kami kembangkan.)

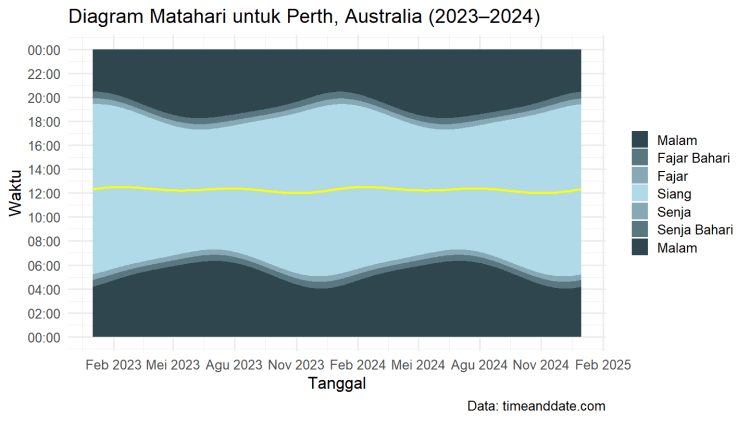
Diagram yang menunjukkan durasi siang dan malam di Perth, Australia selama tahun 2023 hingga 2024, termasuk waktu untuk fajar dan senja. — Gambar 1. Informasi siklus matahari di Kota Perth, Australia

Berdasarkan informasi yang disajikan pada Gambar 1, kita dapat mengekstrak data lamanya siang hari di kota tersebut pada tahun 2023 – 2024. Caranya adalah dengan mengurangi kapan siang harinya berakhir dengan kapan siang harinya mulai. Misalnya, dari Gambar 1 tersebut kita dapat mengamati bahwa pada bulan Desember (puncak musim panas di Perth) siang harinya cenderung lebih lama dibandingkan bulan-bulan lainnya. Pada bulan ini, rerata lama siang harinya adalah sekitar 14,2 jam. Sebagai ilustrasi, pada tanggal 22 Desember 2023, matahari terbit di Perth terjadi pada pukul 05:07 dan terbenamnya pada pukul 19:22 waktu setempat.

Sebaliknya, lamanya siang hari pada bulan Juni (puncak musim dingin di Perth) cenderung lebih singkat dibandingkan bulan-bulan lainnya. Rerata lamanya siang hari pada bulan Juni adalah sekitar 10,1 jam. Agar lebih mudah dibayangkan, pada tanggal 21 Juni 2023, matahari terbit di Perth terjadi pada pukul 07:16 sedangkan terbenamnya pada pukul 17:19.

Setelah mencapai capaian pembelajaran yang disebutkan sebelumnya, peserta didik diharapkan mampu mendeskripsikan, memprediksi, dan mengomunikasikan lamanya siang hari di Perth tersebut sebagai fungsi trigonometri. Fungsi trigonometri tersebut memiliki karakteristik sebagai berikut.

Daerah asalnya bukanlah sudut yang dimulai dari 0° sampai 90°, yaitu sudut-sudut dalam segitiga siku-siku.
Bahkan, daerah asalnya bukanlah sudut! Fungsi tersebut memiliki daerah asal berupa bilangan real yang merepresentasikan waktu. (Detail fungsi ini akan dibahas pada bagian berikutnya.)

Oleh karena itu, peserta didik perlu memperluas pengetahuannya tentang perbandingan trigonometri segitiga siku-siku. Mereka perlu memelajari fungsi trigonometri untuk sembarang bilangan real, yang secara lebih detail dinyatakan dalam capaian pembelajaran sebelumnya.

Pertanyaan berikutnya, bagaimana kita perlu mendesain pembelajaran agar pada akhirnya peserta didik mencapai capaian pembelajaran tersebut? Bagian-bagian berikutnya akan memberikan rekomendasi tentang alur pembelajaran berdasarkan buku yang kami susun, Matematika Tingkat Lanjut untuk SMA/MA Kelas XI (Edisi Revisi). Alur pembelajaran tersebut akan disajikan menurut judul subbab Fungsi Trigonometri dalam buku tersebut: (1) fungsi trigonometri dan lingkaran satuan; (2) grafik fungsi trigonometri; (3) identitas trigonometri; (4) Aturan Sinus; dan (5) Aturan Kosinus.

Fungsi Trigonometri dan Lingkaran Satuan

Langkah pertama, peserta didik perlu memperluas pengetahuannya terhadap ukuran sudut. Mereka perlu mengenal ukuran sudut selain derajat, yaitu radian. Ukuran radian ini merupakan pintu masuk penggunaan fungsi trigonometri untuk sembarang bilangan real (tidak hanya untuk sudut). Mengapa demikian? Perhatikan sudut α pada Gambar 2!

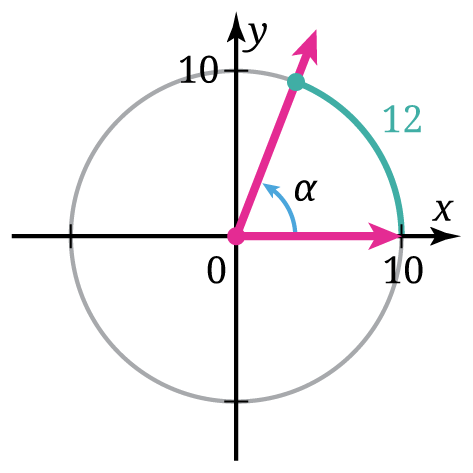
Diagram yang menunjukkan sudut pusat _α_ dari sebuah lingkaran satuan yang berjari-jari 10 satuan. Sudut tersebut menghadap busur lingkaran yang panjangnya 12 satuan. — Gambar 2. Sudut α

Berdasarkan definisinya, ukuran radian menggunakan karakteristik lingkaran. Misalnya, sudut pusat α pada Gambar 2 menghadap busur lingkaran dengan panjang 12 satuan panjang pada sebuah lingkaran dengan jari-jari 10 satuan panjang. Berdasarkan definisi radian, besarnya sudut ini ditentukan dengan membagi panjang busur di depannya dengan jari-jari lingkarannya, yaitu 12/10 = 1,2. Fakta menariknya, sudut yang dinyatakan ke dalam radian ini tidak memiliki satuan! (Berbeda dengan ukuran derajat yang memiliki satuan °.) Hal ini dikarenakan nilai 1,2 tersebut diperoleh dari membagi panjang busur (satuan panjang) dengan jari-jari (yang juga merupakan satuan panjang). Nilai 1,2 tersebut dapat dimaknai seperti berikut: busur lingkaran di depan sudut α panjangnya 1,2 kalinya jari-jari lingkarannya. Nilai 1,2 tersebut tidak memiliki satuan. Dengan demikian, secara umum ukuran radian tidak memiliki satuan dan “murni” bilangan real.

Selain dapat digunakan sebagai pintu masuk untuk menggunakan bilangan real dalam fungsi trigonometri, ukuran radian juga memberikan landasan penting dalam pendefinisian fungsi trigonometri. Landasan tersebut adalah penggunaan pendekatan lingkaran satuan. Dengan menggunakan pendekatan ini, fungsi trigonometri akan memiliki potensi untuk memodelkan dan menyelesaikan berbagai permasalahan yang lebih luas.

Bagaimana mengenalkan fungsi trigonometri dengan menggunakan pendekatan lingkaran satuan kepada peserta didik? Kami mengajak peserta didik bereksplorasi dan menggunakan pengetahuan awalnya tentang perbandingan trigonometri segitiga siku-siku untuk menentukan koordinat beberapa titik pada lingkaran satuan. Perhatikan Gambar 3.

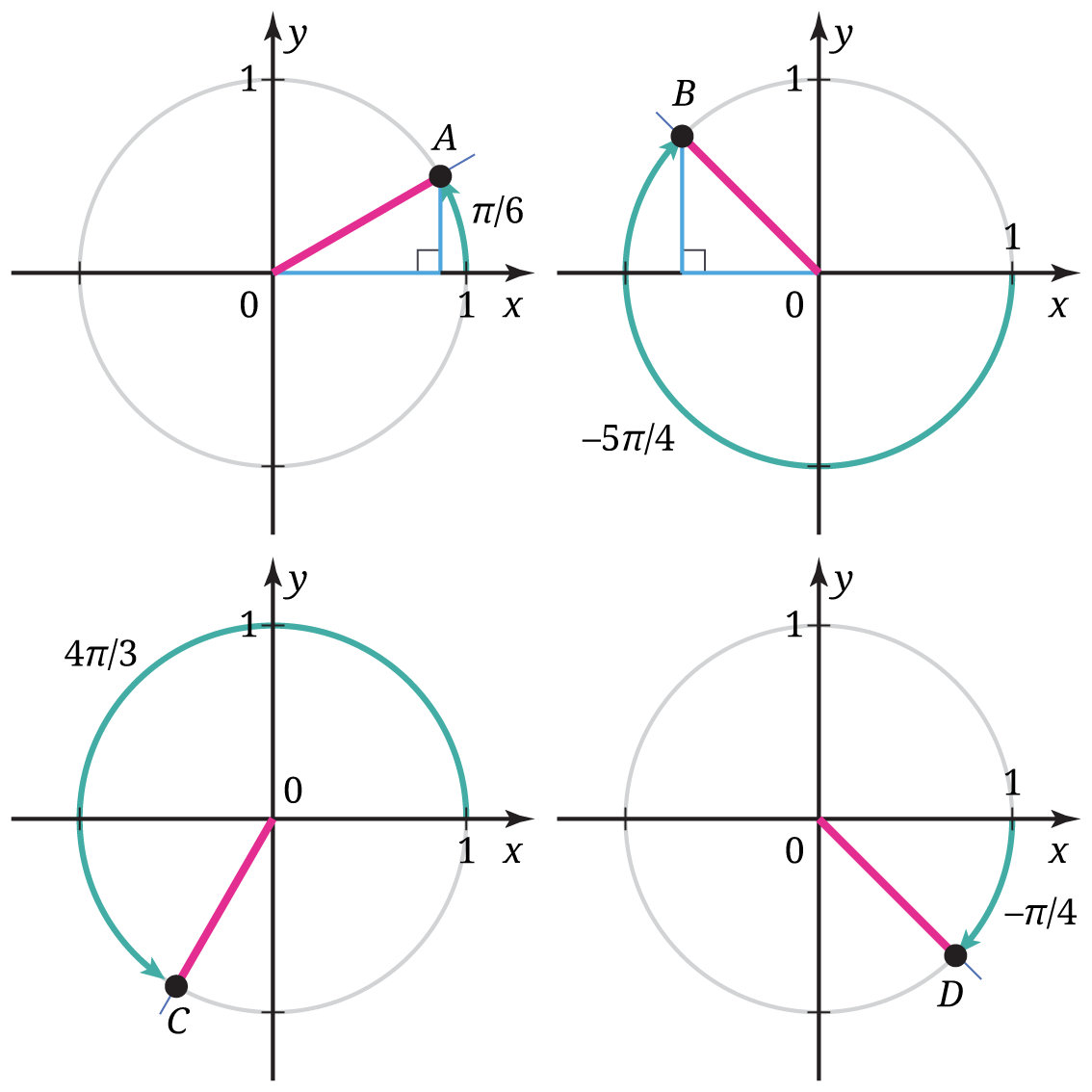
Diagram lingkaran satuan yang menunjukkan sudut pi/6, -5pi/4, 4pi/3, dan -pi/4. — Gambar 3. Titik-titik pada lingkaran satuan

Berdasarkan pengamatannya terhadap Gambar 3, peserta didik diminta untuk menentukan koordinat titik-titik A, B, C, dan D. Untuk menentukan koordinat titik A, peserta didik diharapkan dapat menggunakan perbandingan trigonometri segitiga siku-siku secara langsung, seperti berikut.

$\displaystyle x=r\cos \theta =1\cdot \cos \left( {\frac{\pi }{6}} \right)=\cos \left( {30{}^\circ } \right)=\frac{{\sqrt{3}}}{2}$

$\displaystyle y=r\sin \theta =1\cdot \sin \left( {\frac{\pi }{6}} \right)=\sin \left( {30{}^\circ } \right)=\frac{1}{2}$

Dengan demikian, koordinat titik A adalah $\displaystyle \left( {{{\sqrt{3}}}/{2}\;,{1}/{2}\;} \right)$ . Untuk menentukan koordinat titik-titik B, C, dan D, peserta didik diharapkan dapat menggunakan strategi yang serupa tetapi dengan penambahan satu langkah. Satu langkah tersebut adalah pembuatan sebuah segitiga siku-siku pada kuadran pertama yang salah satu sisinya berimpit dengan sumbu-x dan kongruen dengan segitiga siku-siku yang sisi miringnya adalah $\displaystyle \overline{{OB}}$ , $\displaystyle \overline{{OC}}$ , atau $\displaystyle \overline{{OD}}$ dan sisi lainnya berimpit dengan sumbu-x. Dengan cara seperti ini, peserta didik akan terekspos dengan konsep fungsi trigonometri untuk sembarang bilangan real dan bagaimana cara penentuannya.

Strategi yang dimiliki peserta didik pada kegiatan eksplorasi sebelumnya dapat dijadikan jembatan bagi guru untuk mengenalkan definisi fungsi trigonometri (kosinus, sinus, tangen, sekan, kosekan, dan kotangen) dan strategi bagaimana menentukan fungsi trigonometri dengan menggunakan bilangan acuan.

Definisi Fungsi-Fungsi Trigonometri

Misalkan t adalah sembarang bilangan real dan P(x, y) adalah titik pada lingkaran satuan yang bersesuaian dengan sudut pusat t, seperti yang ditunjukkan pada Gambar 4.

Gambar 4. Sudut pusat t dan titik P(x, y)

Fungsi-fungsi trigonometri kosinus, sinus, tangen, sekan, kosekan, dan kotangen secara berturut-turut didefinisikan sebagai berikut.

$\displaystyle \cos t=x$

$\displaystyle \sin t=y$

$\displaystyle \tan t=\frac{y}{x};\,x\ne 0$

$\displaystyle \sec t=\frac{1}{x};\,x\ne 0$

$\displaystyle \csc t=\frac{1}{y};\,y\ne 0$

$\displaystyle \cot t=\frac{x}{y};\,y\ne 0$

Bilangan acuan sangat manjur dimanfaatkan untuk menentukan nilai fungsi trigonometri sembarang bilangan real asalkan kita mengetahui nilai fungsi trigonometri yang bersesuaian untuk bilangan acuan tersebut. Sebagai ilustrasi, perhatikan Gambar 5.

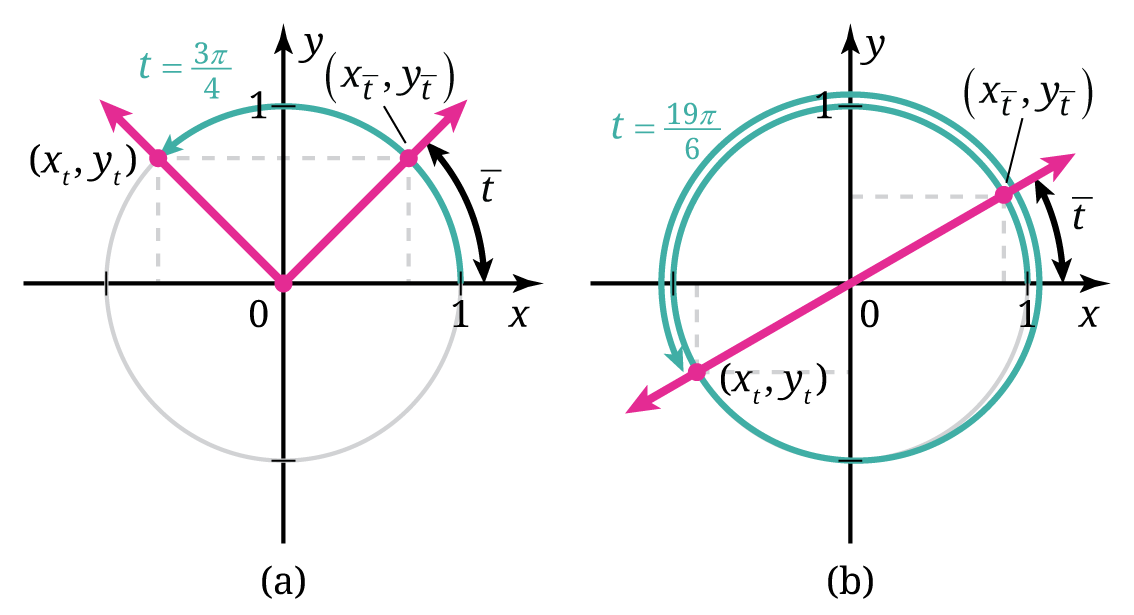
Gambar 5. Bilangan real t dan bilangan acuan yang bersesuaian

Misalkan kita akan menentukan nilai $\displaystyle \cos \left( {{{3\pi }}/{4}\;} \right)$ dan $\displaystyle \sin \left( {{{19\pi }}/{6}\;} \right)$ . Berdasarkan Gambar 5(a), kita tahu bahwa bilangan acuan $\displaystyle t={{3\pi }}/{4}\;$ adalah $\displaystyle \overline{t}=\pi -{{3\pi }}/{4}\;={\pi }/{4}\;$ . Dengan menggunakan definisi fungsi trigonometri, kita dapat menentukan nilai kosinus $\displaystyle t={{3\pi }}/{4}\;$ seperti berikut.

$\displaystyle \cos \left( {\frac{{3\pi }}{4}} \right)={{x}_{t}}=-{{x}_{{\overline{t}}}}=-\cos \left( {\frac{\pi }{4}} \right)=-\frac{{\sqrt{2}}}{2}$

Dengan cara yang serupa, kita dapat menentukan nilai $\displaystyle \sin \left( {{{19\pi }}/{6}\;} \right)$ dengan menggunakan Gambar 5(b) seperti berikut.

$\displaystyle \sin \left( {\frac{{19\pi }}{6}} \right)={{y}_{t}}=-{{y}_{{\overline{t}}}}=-\sin \left( {\frac{\pi }{6}} \right)=-\frac{1}{2}$

Ide dasar penentuan nilai fungsi trigonometri untuk $\displaystyle t={{3\pi }}/{4}\;$ dan $\displaystyle {{19\pi }}/{6}\;$ tersebut sebenarnya telah dimiliki peserta didik ketika menyelesaikan permasalahan pada Gambar 3, tetapi dengan penambahan pengetahuan tentang definisi fungsi trigonometri dengan menggunakan pendekatan lingkaran satuan.

Setelah peserta didik fasih menggunakan bilangan acuan untuk menentukan nilai fungsi trigonometri, kami mengenalkan sifat fungsi genap dan fungsi ganjil untuk fungsi trigonometri. Hal ini dimaksudkan agar peserta didik memiliki cukup repertoar untuk menentukan nilai fungsi trigonometri. Selain itu, sifat tersebut akan membantu mereka untuk menyelidiki karakteristik fungsi trigonometri.

Untuk mengenalkan sifat fungsi genap dan fungsi ganjil tersebut, kami menyediakan media pembelajaran digital yang dapat dimanfaatkan peserta didik untuk menyelidiki nilai-nilai fungsi trigonometri. Media tersebut dikembangkan di kalkulator grafik Desmos dan dapat diakses melalui tautan https://s.id/trig-genap-ganjil. Tangkapan layarnya dapat dilihat pada Gambar 6.

Gambar 6. Tangkapan layar media pembelajaran sifat fungsi genap dan fungsi ganjil

Setelah bereksplorasi menggunakan media pembelajaran yang ditampilkan pada Gambar 6, peserta didik diharapkan dapat membuat konjektur seperti berikut.

$\displaystyle \sin \left( {-t} \right)=-\sin t$ , $\displaystyle \cos \left( {-t} \right)=\cos t$ , dan $\displaystyle \tan \left( {-t} \right)=-\tan t$

Dengan menggunakan definisi fungsi trigonometri, peserta didik dapat memperluas sifat fungsi genap dan fungsi ganjil tersebut terhadap fungsi kosekan, sekan, dan kotangen.

$\displaystyle \csc \left( {-t} \right)=-\csc t$ , $\displaystyle \sec \left( {-t} \right)=\sec t$ , dan $\displaystyle \cot \left( {-t} \right)=-\cot t$

Dengan sifat ini, peserta didik dapat menentukan nilai fungsi trigonometri untuk bilangan-bilangan real yang negatif. Misalnya, mereka dapat menggunakan sifat ini untuk menentukan nilai fungsi trigonometri berikut.

$\displaystyle \sin \left( {-\frac{\pi }{4}} \right)=-\sin \left( {\frac{\pi }{4}} \right)=-\frac{{\sqrt{2}}}{2}$

Grafik Fungsi Trigonometri

Sampai pada tahap ini, peserta didik telah menyadari bahwa fungsi trigonometri dapat ditentukan nilainya untuk sembarang bilangan real yang masuk ke dalam daerah asalnya. Selanjutnya, mereka perlu mengetahui bagaimana bermanfaatnya fungsi tersebut dalam memodelkan dan menyelesaikan berbagai macam permasalahan.

Salah satu kegunaan fungsi trigonometri adalah untuk memodelkan dan menyelesaikan permasalahan pasang surut air laut. Perhatikan permasalahan berikut.

Pada suatu hari, ketinggian permukaan air Teluk Kupang 0,4 m di atas rata-rata permukaan airnya ketika pasang dan menjadi 0,4 di bawah rata-rata permukaan airnya ketika surut. Pada hari itu, teluk ini mengalami dua kali pasang dan dua kali surut. Pada pukul 00.00 ketinggian permukaan air sama dengan ketinggian rata-ratanya. Berikut ini, lihat Gambar 7, grafik ketinggian (dalam m) permukaan air Teluk Kupang setiap x jam setelah pukul 00.00.

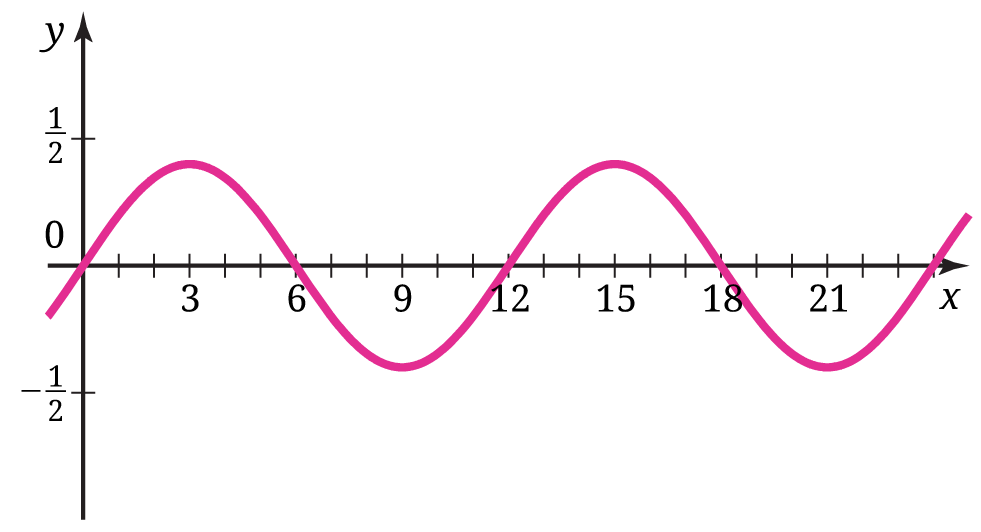
Gambar 7. Ketinggian permukaan air Teluk Kupang

Carilah fungsi y = a sin bx yang memodelkan ketinggian permukaan air Teluk Kupang setiap waktunya.
Dengan menggunakan fungsi pada nomor 1, perkirakan ketinggian permukaan air teluk tersebut pada pukul 16.00.

Permasalahan Teluk Kupang di atas kurang lebih serupa dengan permasalahan durasi siang hari Kota Perth yang disajikan di awal. Untuk dapat menyelesaikan permasalahan-permasalahan tersebut, peserta didik perlu memahami bagaimana karakteristik fungsi trigonometri (dalam kasus ini adalah fungsi kosinus dan sinus). Karakteristik fungsi tersebut akan lebih mudah dilihat dengan menyelidiki grafiknya.

Agar peserta didik memahami grafik fungsi trigonometri, pertama-tama kami mengajak mereka secara “informal” untuk mensketsa situasi yang melibatkan fungsi trigonometri. Situasi tersebut adalah situasi tentang jarak tempuh dan ketinggian seseorang ketika bermain kincir ria, seperti yang diejawantahkan ke dalam permasalahan eksploratif berikut.

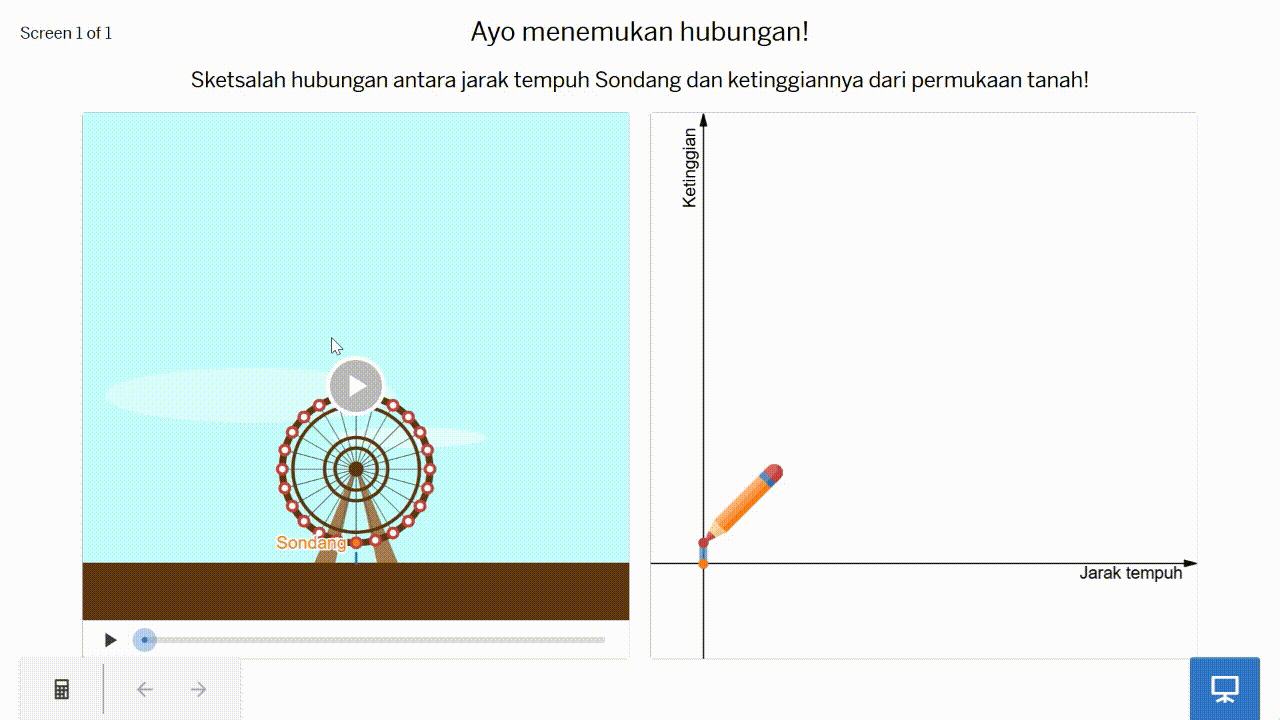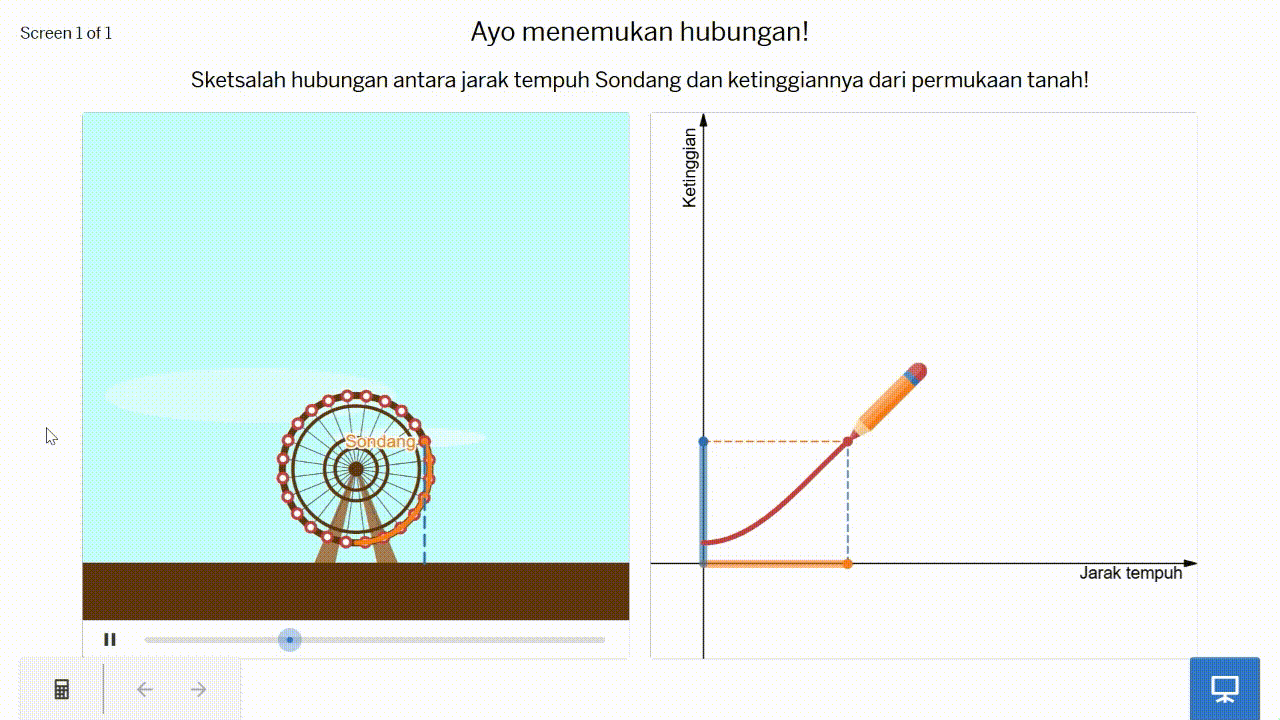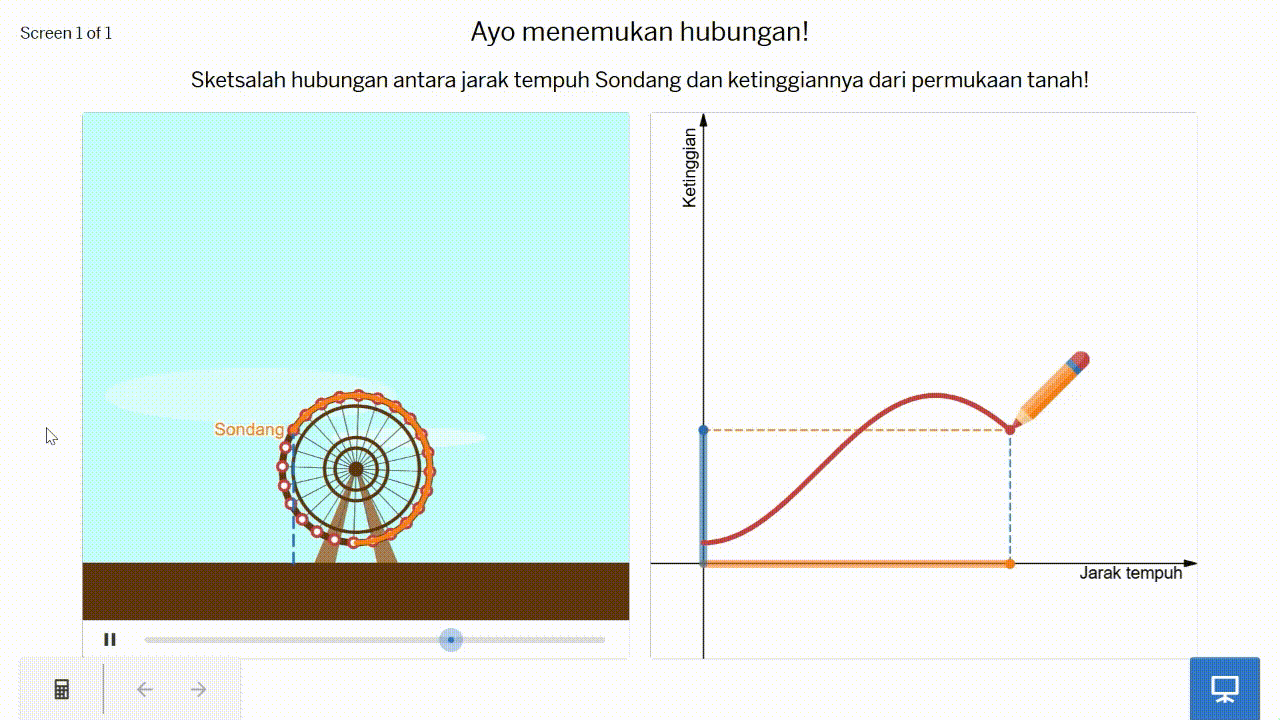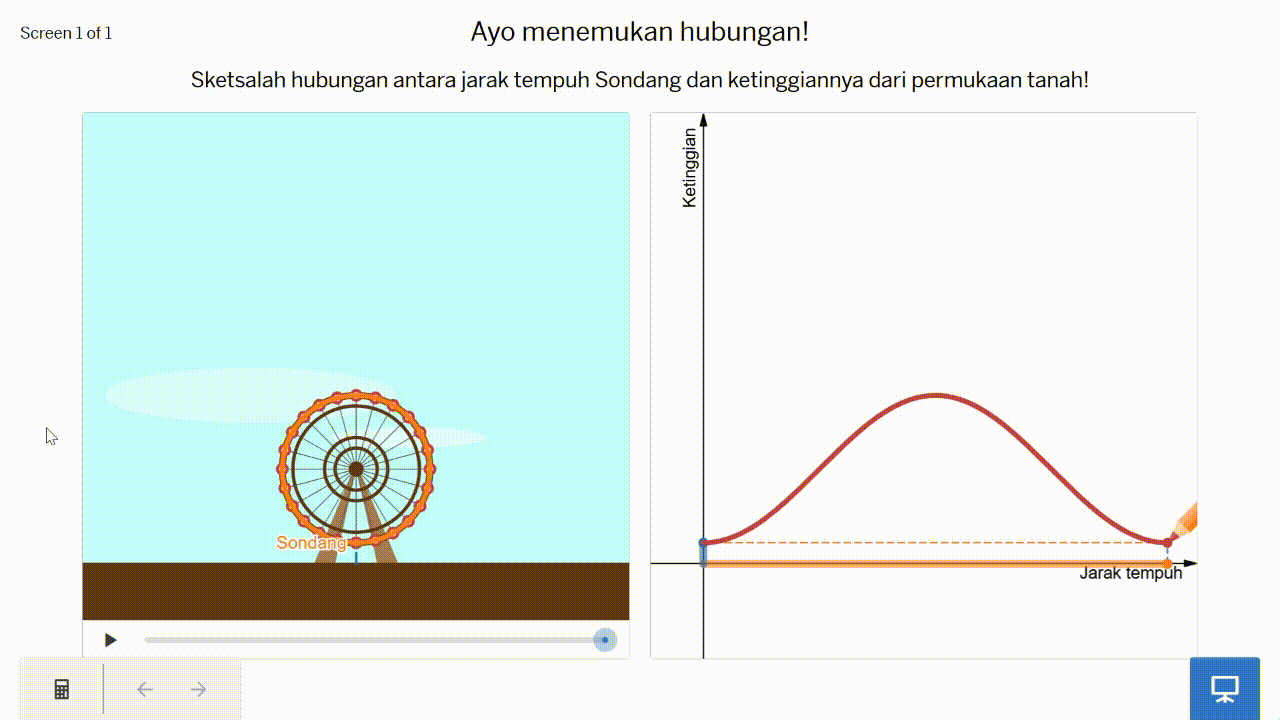
Ketika di pasar malam, Sondang naik kincir ria. Mula-mula, dia berada di bagian bawah kincir ria tersebut. Ketika kincir ria berputar, jarak tempuh dan ketinggian Sondang berubah-ubah. Perhatikan Gambar 8!

Gambar 8. Jarak tempuh dan ketinggian Sondang

Sketsalah hubungan antara jarak tempuh dan ketinggian Sondang dalam kincir ria tersebut pada Gambar 9!

Gambar 9. Bidang koordinat untuk mensketsa hubungan antara jarak tempuh dan tinggi

Pada permasalahan kincir ria tersebut, peserta didik diharapkan dapat mengkoordinasikan dua kuantitas yang berubah secara bersama-sama, yaitu jarak tempuh dan ketinggian Sondang, dan merepresentasikannya ke dalam sebuah grafik. Harapannya, peserta didik dapat mensketsa grafik yang kurang lebih diilustrasikan pada Gambar 10.

Gambar 10. Salah satu kemungkinan proses sketsa peserta didik

Ketika peserta didik mampu mensketsa grafik seperti pada Gambar 10, mereka dapat membayangkan bahwa jarak tempuh dan ketinggian Sondang dapat direpresentasikan sebagai dua ruas garis pada sumbu-x dan sumbu-y yang salah satu ujungnya di titik asal (0, 0). Setelah itu, mereka memahami sebuah grafik sebagai jejak titik yang pergerakannya dibatasi oleh panjang kedua ruas garis yang merepresentasikan jarak tempuh dan ketinggian tersebut.

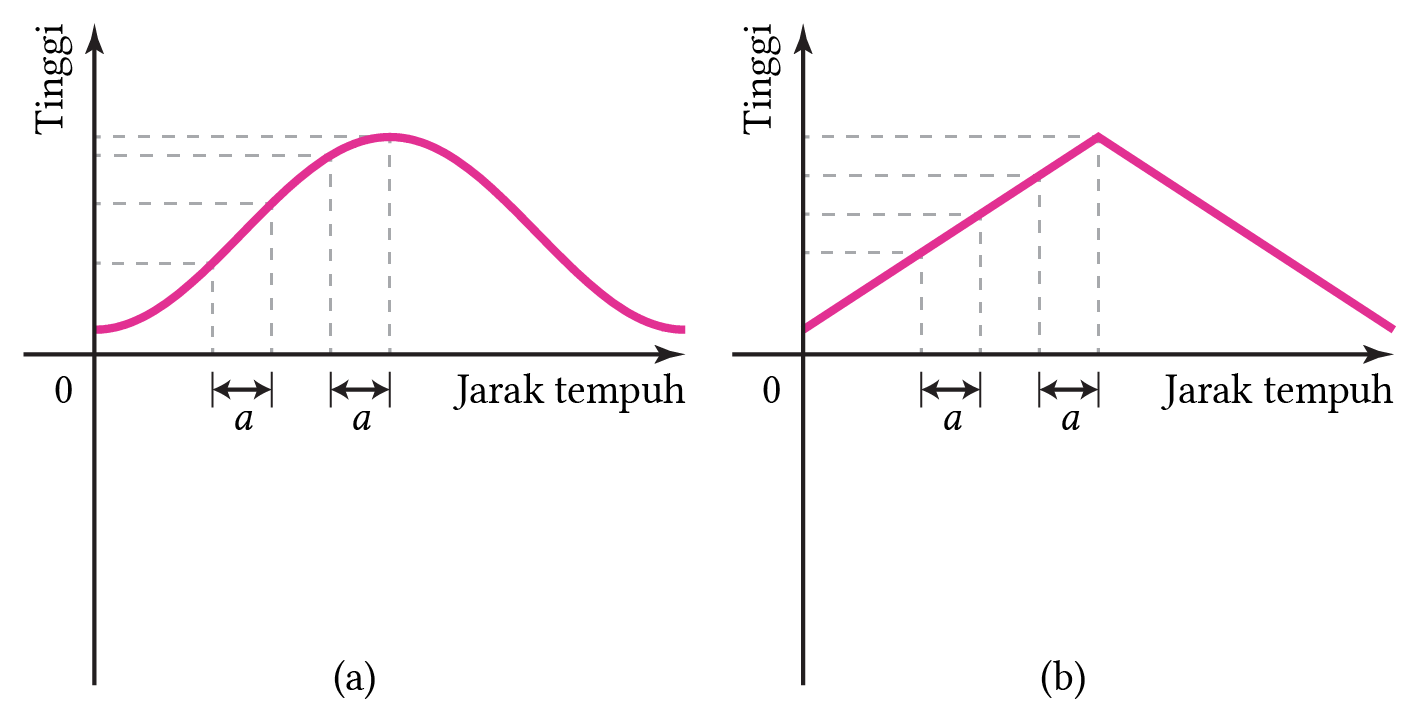
Untuk memperdalam pemahaman peserta didik, mereka dapat diberikan pertanyaan lanjutan. Misalnya, mereka dapat diminta untuk memerhatikan Gambar 11 berikut kemudian ditanya, “Mengapa grafik (a) lebih tepat merepresentasikan hubungan antara jarak tempuh dan ketinggian Sondang selama dia di kincir ria?” Dengan pertanyaan seperti ini, mereka diharapkan dapat bernalar secara lebih detail tentang hubungan antara jarak tempuh dan ketinggian Sondang.

Gambar 11. Dua kemungkinan grafik hubungan jarak tempuh dengan ketinggian

Permasalahan kincir ria tersebut memuat ide dasar tentang bagaimana melukis grafik fungsi trigonometri. Untuk mengenalkan strategi melukis grafik fungsi trigonometri, pertama kami mengajak peserta didik untuk melakukan plot titik. Kami memilih strategi ini agar sesuai dengan pengetahuan awal peserta didik tentang bagaimana melukis grafik sebuah fungsi. Setelah itu, kami juga mengenalkan strategi melukis grafik fungsi trigonometri dengan menggunakan lingkaran satuan. Perhatikan Gambar 12.

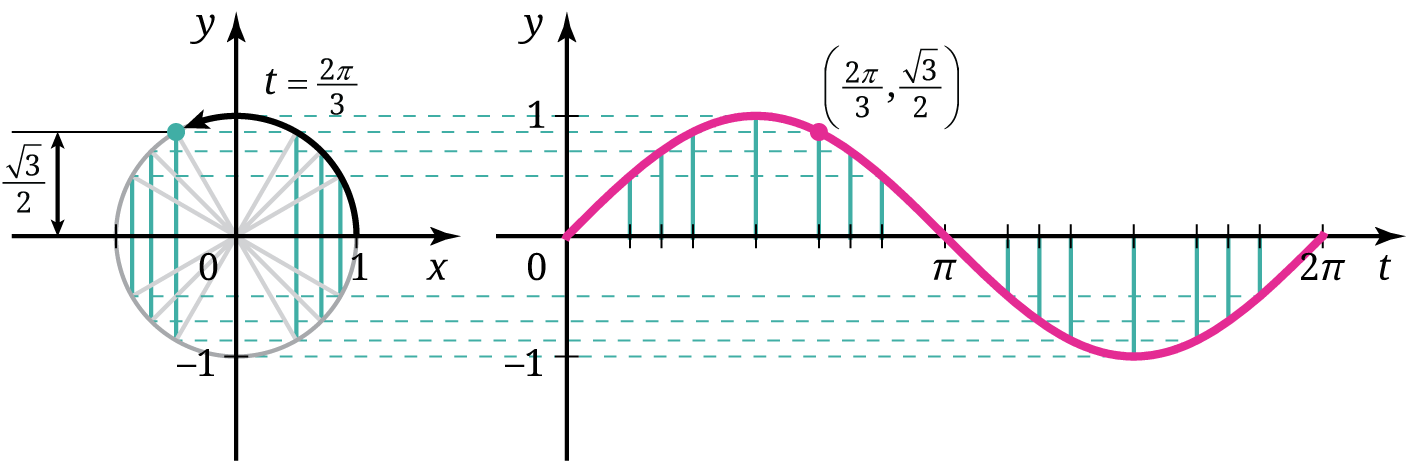
Gambar 12. Grafik fungsi y = sin t untuk 0 ≤ t ≤ 2π

Strategi yang diilustrasikan pada Gambar 12 dibangun oleh pengalaman belajar peserta didik sebelumnya tentang ukuran sudut radian, definisi fungsi trigonometri dengan pendekatan lingkaran satuan, dan strategi melukis grafik pada permasalahan kincir ria. Jika memungkinkan, peserta didik juga dapat mengakses media pembelajaran digital yang memperjelas strategi pada Gambar 12 tersebut. Media pembelajaran tersebut dapat diakses di https://s.id/sin-lingkaran dan tangkapan layarnya ditunjukkan pada Gambar 13.

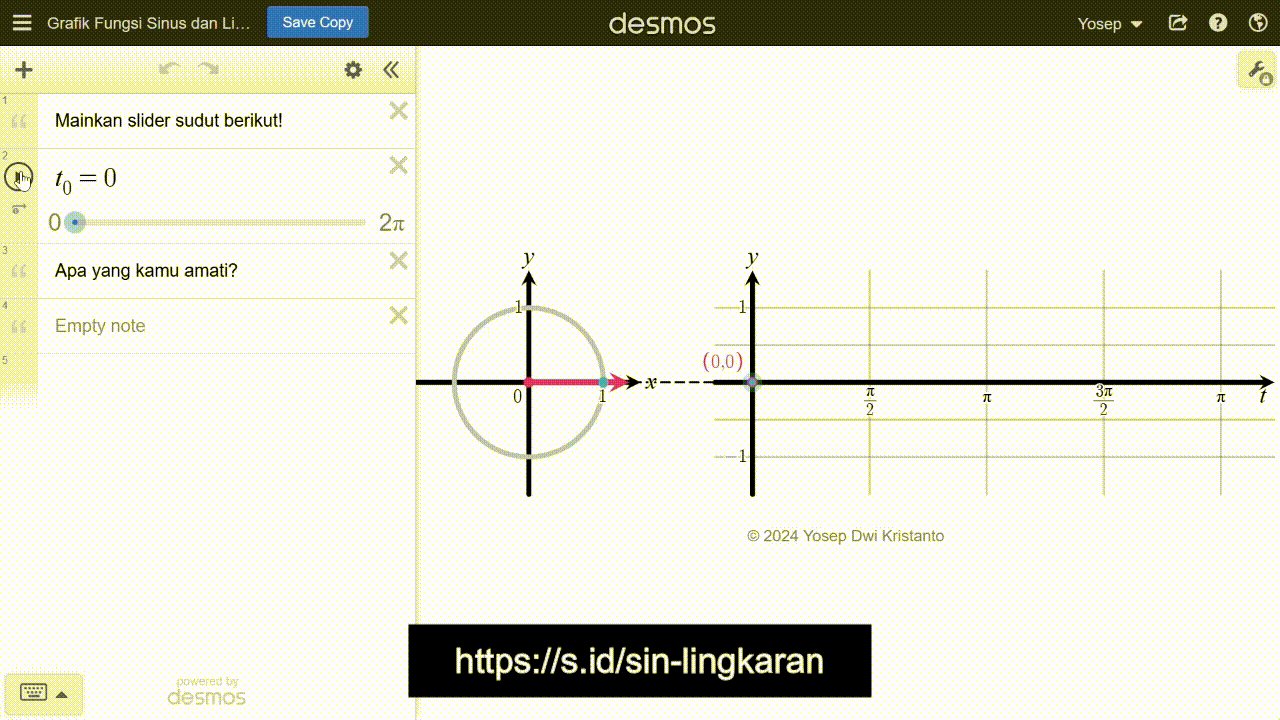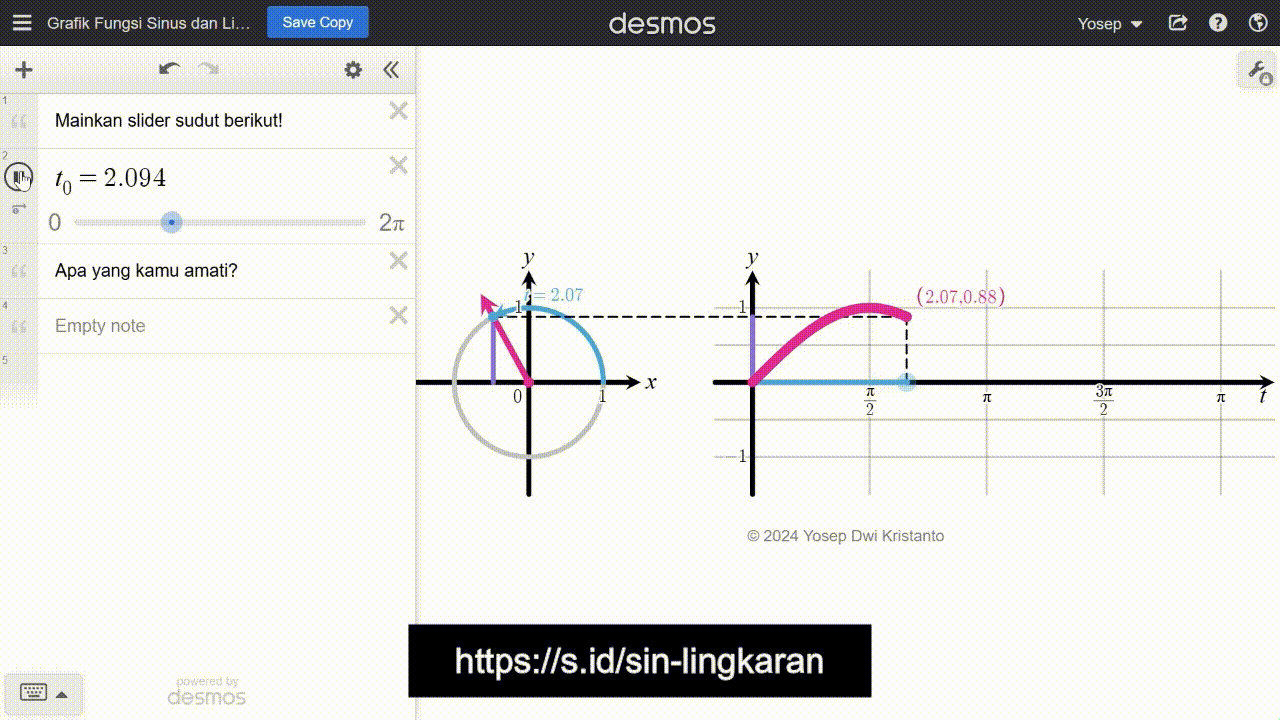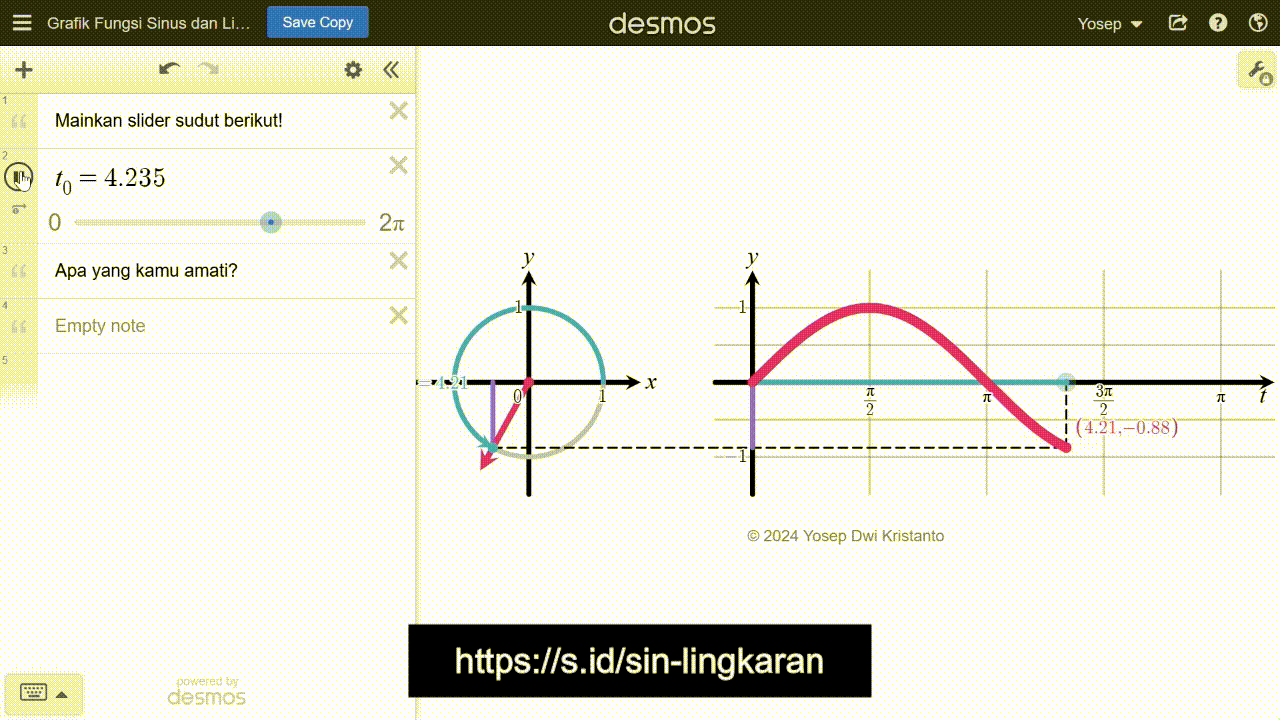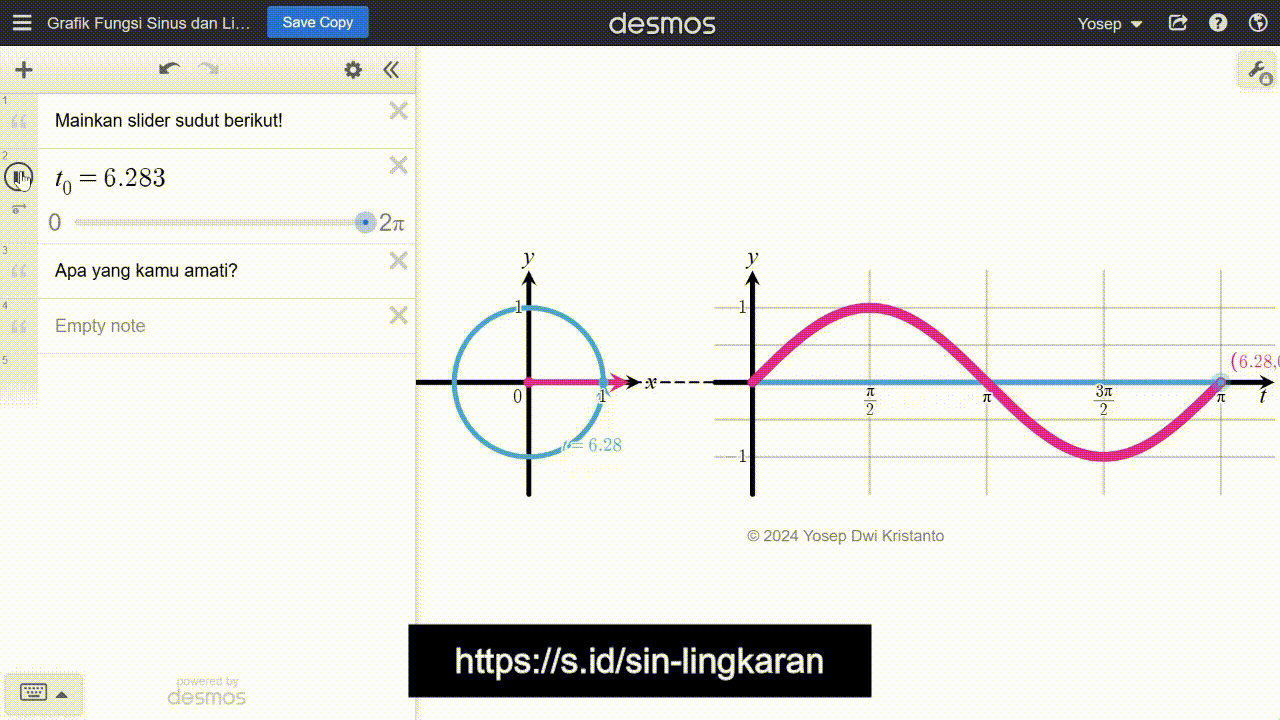
Gambar 13. Sketsa grafik fungsi fungsi sinus dengan lingkaran satuan

Grafik fungsi sinus yang ditunjukkan pada Gambar 12 maupun 13 hanya merentang mulai dari 0 sampai 2π. Peserta didik perlu menyadari bahwa mereka dapat melanjutkan grafik tersebut ke kanan atau kiri secara tak hingga. Hal ini serupa untuk grafik fungsi kosinus. Secara umum, grafik fungsi sinus dan kosinus secara berturut-turut diperlihatkan pada Gambar 14 dan 15.

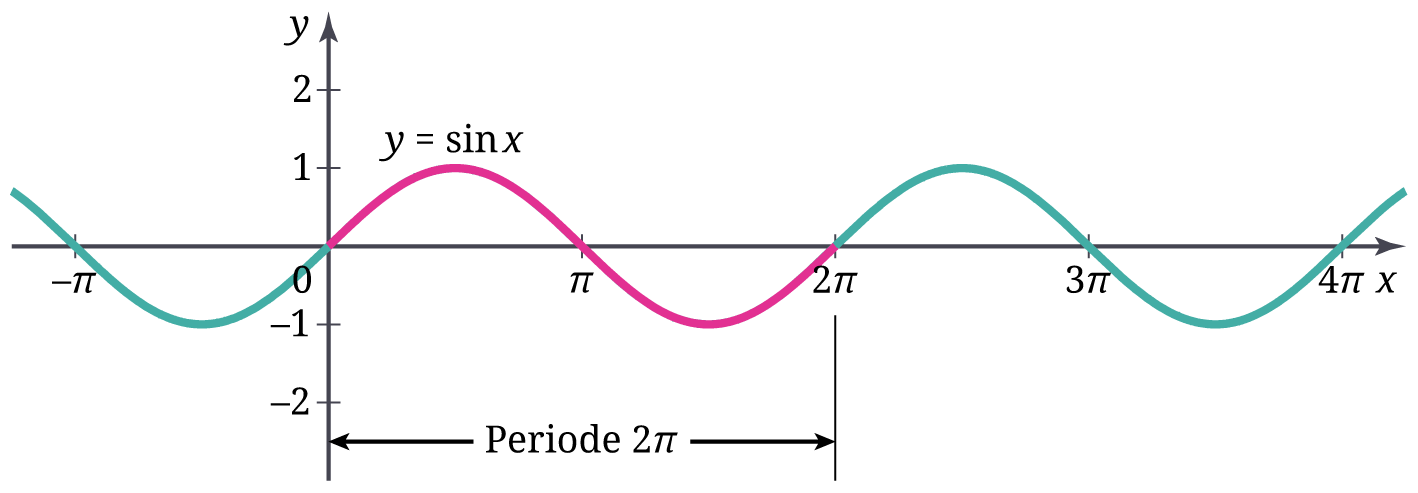
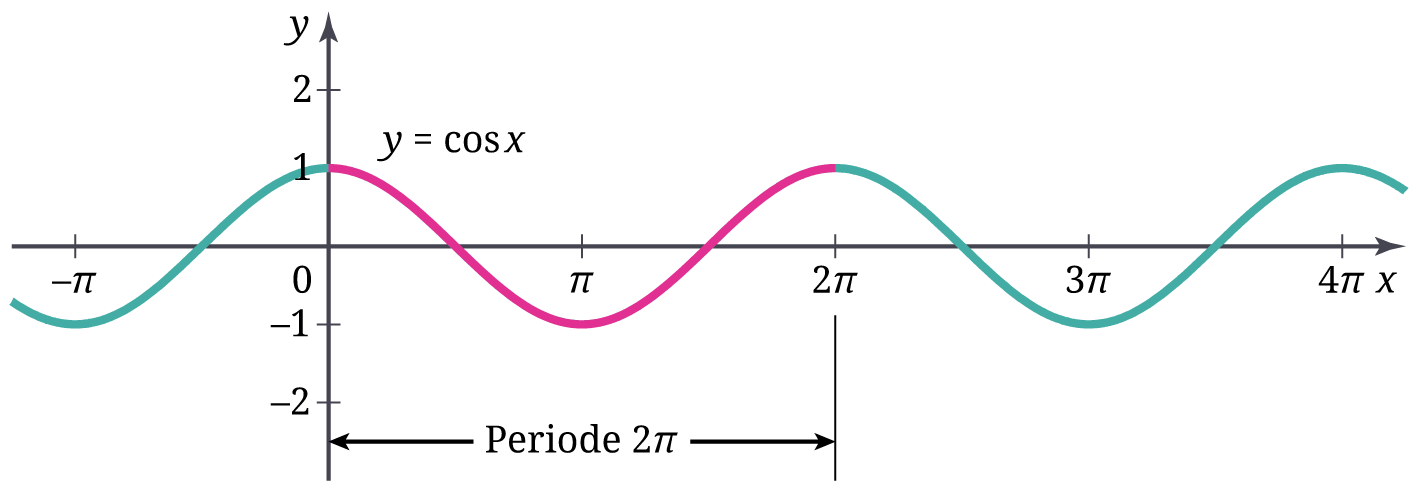
Berdasarkan Gambar 14 dan 15 tersebut, peserta didik perlu dipandu untuk mengamati salah satu karakteristik fungsi trigonometri—bahwa fungsi ini periodik. Nilai fungsi trigonometri berulang setiap periode tertentu. Berdasarkan kedua gambar tersebut, mereka perlu memahami bahwa baik fungsi sinus maupun kosinus memiliki periode 2π. Dengan kata lain, nilai fungsi sinus dan kosinus berulang setiap 2π.

Fungsi sinus dan kosinus banyak sekali variannya. Untuk memahami semua kemungkinan variannya, kami menggunakan konsep transformasi fungsi. Dengan konsep ini, peserta didik diharapkan dapat menghubungkan varian fungsi sinus dan kosinus dengan menggunakan fungsi dasarnya, y = sin x dan y = cos x, dan memahami karakteristiknya seperti amplitudo, periode, pergeseran horizontal, dan pergeseran vertikal.

Transformasi Fungsi Sinus dan Kosinus

Fungsi sinus: $\displaystyle y=a\sin k\left( {x-b} \right)+c$ dengan $\displaystyle k>0$
Fungsi kosinus: $\displaystyle y=a\cos k\left( {x-b} \right)+c$ dengan $\displaystyle k>0$
Grafik kedua fungsi tersebut memiliki amplitudo $\displaystyle \left| a \right|$ , periode $\displaystyle {{2\pi }}/{k}\;$ , pergeseran horizontal b, dan pergeseran vertikal c.

Untuk memperdalam pengetahuan peserta didik tentang varian fungsi sinus dan kosinus dengan menggunakan transformasi fungsi, kami selanjutnya menyediakan permasalahan yang memantik kreativitas mereka. Permasalah tersebut adalah sebagai berikut.

Diberikan grafik seperti pada Gambar 16 berikut.

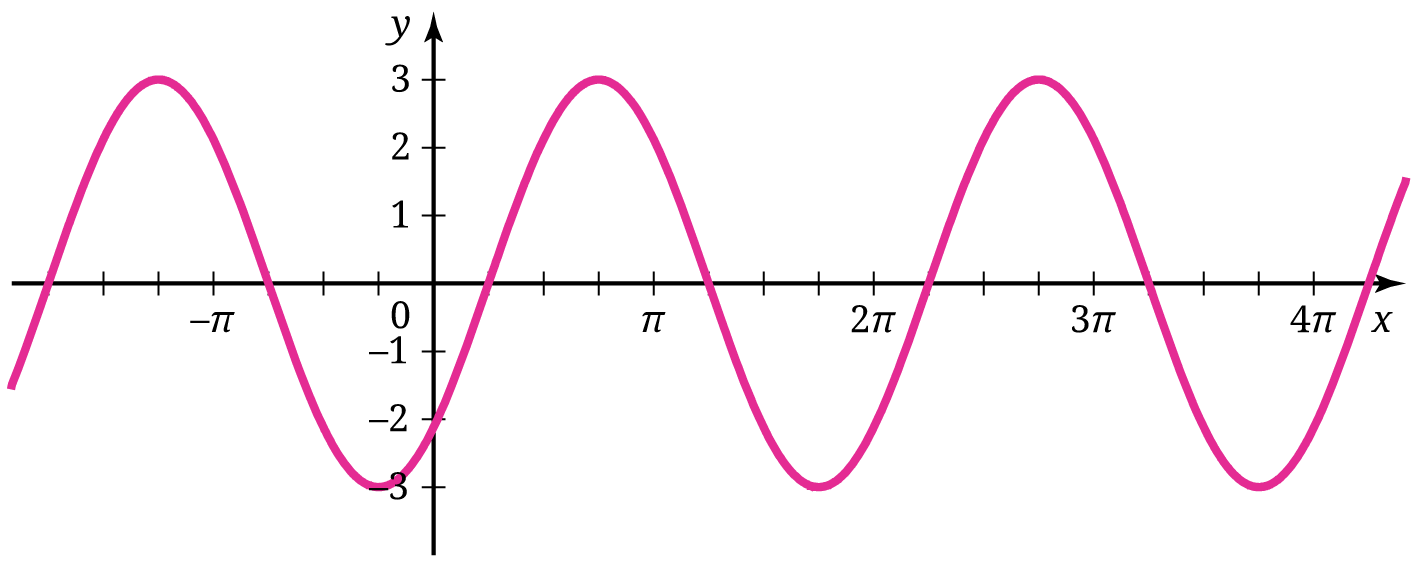
Dhien menganggap bahwa grafik tersebut merupakan grafik fungsi $\displaystyle y=3\sin \left( {x-\frac{\pi }{4}} \right)$ , sedangkan Ahmad melihatnya sebagai grafik fungsi $\displaystyle y=3\cos \left( {x-\frac{{3\pi }}{4}} \right)$ . Siapa yang menurut kamu tepat? Mengapa?
Paulina menemukan bahwa grafik pada Gambar 16 merupakan grafik setiap fungsi trigonometri berikut.
$\displaystyle y=3\sin \left( {x-\frac{\pi }{4}} \right)$ , $\displaystyle y=3\sin \left( {x-\frac{{9\pi }}{4}} \right)$ , $\displaystyle y=3\sin \left( {x-\frac{{17\pi }}{4}} \right)$ ,
$\displaystyle y=3\cos \left( {x+\frac{{5\pi }}{4}} \right)$ , $\displaystyle y=3\cos \left( {x-\frac{{3\pi }}{4}} \right)$ , dan $\displaystyle y=3\cos \left( {x-\frac{{11\pi }}{4}} \right)$
Menurutmu, bagaimana Paulina memperoleh persamaan-persamaan fungsi tersebut?

Permasalahan tersebut memiliki dua tujuan utama. Pertama, permasalahan tersebut meminta peserta didik untuk menginterpretasi grafik yang diberikan sebagai transformasi fungsi dasar y = sin ⁡x atau y = cos ⁡x. Kedua, permasalahan tersebut mengajak peserta didik untuk memahami bahwa sebuah kurva sinusoidal dapat direpresentasikan ke dalam banyak varian fungsi sinus maupun kosinus.

Sampai di sini, peserta didik diharapkan mampu mensketsa grafik fungsi dasar fungsi sinus dan kosinus, y = sin x dan y = cos x, dan menganalisis karakteristiknya serta menggunakan kedua grafik tersebut untuk mengonstruksi dan menginterpretasi berbagai macam varian fungsi sinus dan kosinus dengan menggunakan transformasi fungsi. Berbekal kemampuan ini, berikutnya kami mengenalkan grafik fungsi tangen dasar, yaitu y = tan x. Grafik tersebut ditunjukkan pada Gambar 17.

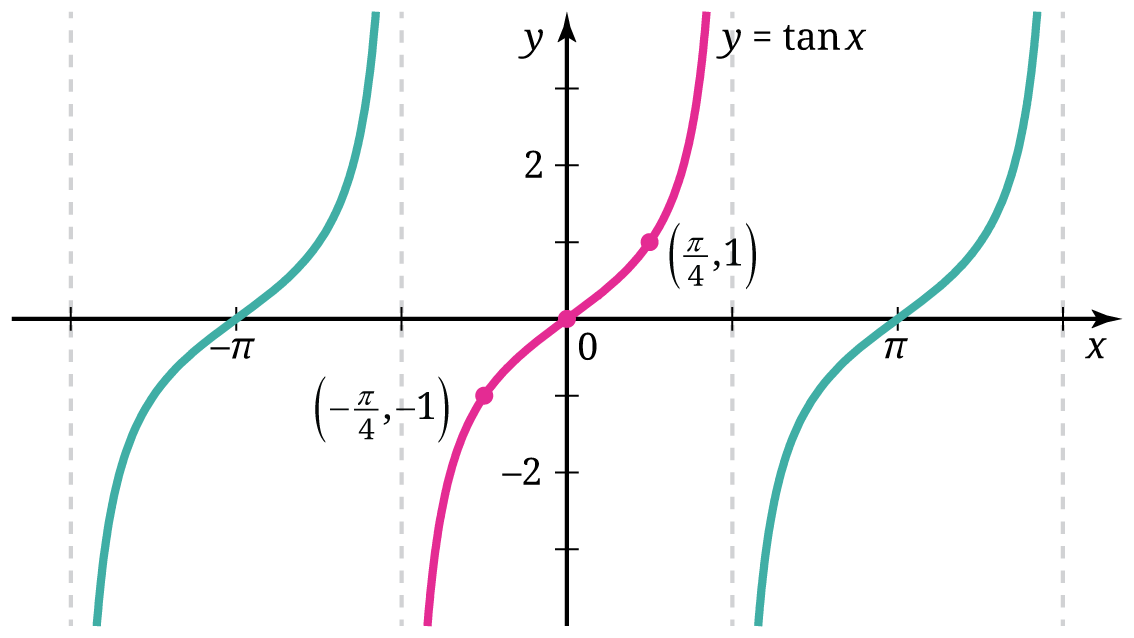
Grafik fungsi tangen pada Gambar 17 tersebut secara signifikan berbeda dengan grafik fungsi sinus dan kosinus. Untuk itu, peserta didik perlu menganalisis karakteristik unik fungsi tangen tersebut. Di antaranya adalah (a) periodenya sebesar π; (b) daerah asalnya berupa himpunan semua bilangan real, kecuali $\displaystyle {\pi }/{2}\;+n\pi$ untuk sembarang bilangan bulat n; dan (c) memiliki asimtot vertikal pada nilai x yang membuat fungsi tersebut tidak terdefinisi.

Setelah memahami grafik fungsi tangen y = tan x dan karakteristiknya, kami mengajak peserta didik untuk menggunakan pengetahuannya tentang transformasi fungsi untuk mengonstruksi grafik varian fungsi tangen, yaitu $\displaystyle f\left( x \right)=\tfrac{1}{2}\tan \left( {x+\tfrac{\pi }{3}} \right)$ . Harapannya, mereka memahami bahwa grafik fungsi f tersebut dapat diperoleh dengan menggeser grafik y = tan x ke kiri sejauh $\displaystyle {\pi }/{3}\;$ satuan, kemudian meregangkannya secara vertikal dengan faktor $\displaystyle {1}/{2}\;$ . Dengan demikian, mereka dapat mensketsa grafik f seperti yang ditunjukkan pada Gambar 18.

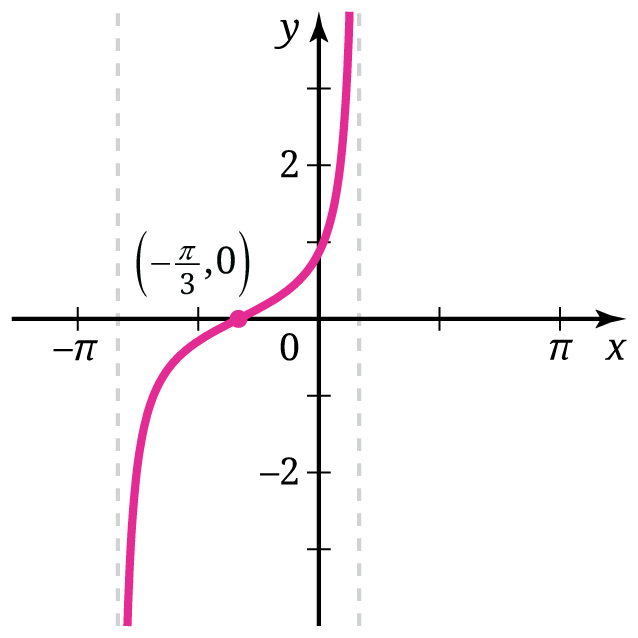
Pemahaman peserta didik tentang grafik fungsi sinus, kosinus, dan tangen pada akhirnya dapat digunakan untuk memodelkan dan menyelesaikan berbagai macam permasalahan yang melibatkan ketiga fungsi tersebut. Misalnya adalah permasalahan durasi siang hari di Kota Perth dan permasalahan Teluk Kupang yang telah disebutkan sebelumnya.

Untuk memodelkan permasalahan lamanya siang hari di Kota Perth, peserta didik dapat ditunjukkan grafik yang menghubungkan waktu dan lamanya siang hari. Hal ini, misalnya, dapat dilakukan dengan memerlihatkan grafik pada kalkulator matahari, seperti yang diilustrasikan pada Gambar 19.

Gambar 19. Grafik lamanya siang hari di Perth pada 2023 – 2024

Berdasarkan eksplorasi kalkulator matahari tersebut, peserta didik diharapkan dapat menemukan informasi kapan lamanya siang hari di Perth maksimum dan minimum. Pada tahun 2023 – 2024, lamanya siang hari maksimum terjadi pada 22-12-2023 dan 21-12-2024. Di dua hari tersebut, lamanya siang hari adalah 14,24556. Lamanya siang hari yang minimum di antara kedua tanggal tersebut terjadi pada 20-06-2024 dan 21-06-2024, yaitu sebesar 10,05611 jam.

Jika peserta didik menggunakan tanggal 31-12-2022 sebagai acuan, lamanya hari maksimum tersebut terjadi 356 dan 721 setelah tanggal acuan tersebut. Dengan menggunakan perkiraan, minimumnya terjadi pada $\displaystyle {{\left( {356+721} \right)}}/{2}\;=\text{538,5}$ . Dengan menggunakan fungsi kosinus sebagai modelnya, periode fungsinya adalah 721 – 356 = 365. Amplitudonya adalah $\displaystyle {{\left( {\text{14,24556}-\text{10,05611}} \right)}}/{2}\;=\text{2,094725}$ . Pergeseran vertikalnya adalah $\displaystyle {{\left( {\text{14,24556}+\text{10,05611}} \right)}}/{2}\;=\text{12,150835}$ . Terakhir, pergeseran horizontalnya adalah 356. Semua informasi tersebut dapat diterjemahkan ke dalam grafik fungsi kosinus seperti yang disajikan pada Gambar 20.

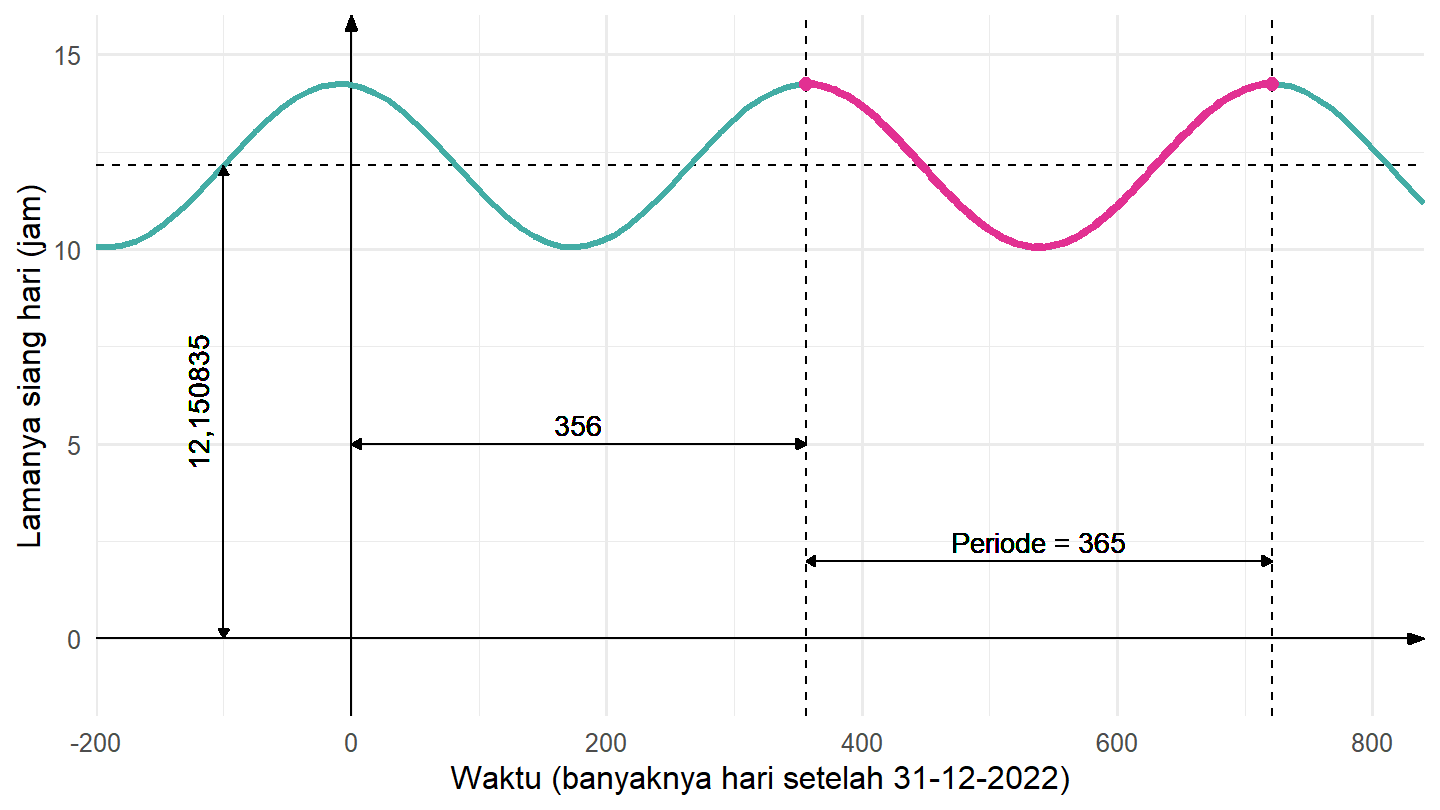
Gambar 20. Model lamanya siang hari di Kota Perth, Australia

Berdasarkan semua informasi ini, fungsi kosinus yang memodelkan lamanya siang hari (jam) di Perth setiap waktunya (dalam hari sejak 31-12-2022) adalah sebagai berikut.

$\displaystyle L\left( x \right)=\text{2}\text{,094725}\cos \left[ {\frac{{2\pi }}{{365}}\left( {x-356} \right)} \right]+\text{12}\text{,150835}$

Sekali lagi, daerah asal fungsi L tersebut adalah himpunan semua bilangan real. Dengan demikian, peserta didik dapat menentukan lamanya hari pada tanggal 24-09-2022 (98 hari sebelum tanggal acuan) dan 24-09-2023 (267 hari setelah tanggal acuan) dengan menggunakan model tersebut sebagai berikut.

$\displaystyle L\left( {-98} \right)=\text{2}\text{,094725}\cos \left[ {\frac{{2\pi }}{{365}}\left( {-98-356} \right)} \right]+\text{12}\text{,150835}\approx \text{12}\text{,2319}$

$\displaystyle L\left( {267} \right)=\text{2}\text{,094725}\cos \left[ {\frac{{2\pi }}{{365}}\left( {267-356} \right)} \right]+\text{12}\text{,150835}\approx \text{12}\text{,2319}$

Kedua nilai tersebut masuk akal karena dari 24-09-2022 sampai 24-09-2023 merentang 365 hari, yang merupakan periode fungsi L, sehingga nilai fungsinya sama. Untuk kedua tanggal itu, nilai fungsinya adalah sekitar 12,2319 jam.

Menyelam Lebih Dalam: Mengevaluasi Model

Untuk memberi ruang kepada peserta didik untuk berpikir kritis, kita dapat memberikan pertanyaan pemantik kepada mereka. Secara khusus, pertanyaan tersebut perlu membuat mereka berpikir ulang terhadap model yang mereka temukan.

Misalkan mereka mendapatkan model fungsi L seperti yang kita temukan sebelumnya. Dengan model tersebut, kita dapat memprediksi lamanya siang hari di Perth pada 31-12-2025 (1096 hari setelah 31-12-2022) dan 31-12-2045 (8401 hari setelah 31-12-2022) seperti berikut.

$\displaystyle L\left( {1096} \right)=\text{2,094725}\cos \left[ {\frac{{2\pi }}{{365}}\left( {1096-356} \right)} \right]+\text{12,150835}\approx \text{14,214600}$

$\displaystyle L\left( {8401} \right)=\text{2,094725}\cos \left[ {\frac{{2\pi }}{{365}}\left( {8401-356} \right)} \right]+\text{12,150835}\approx \text{14,176115}$

Seberapa baik model kita tersebut? Untuk menjawabnya, kita dapat membandingkannya dengan data di timeanddate.com. Berdasarkan situs web tersebut, lamanya siang hari di Perth pada 31-12-2025 dan 31-12-2045 secara berturut-turut adalah 14:12:30 (atau sekitar 14,208333 jam) dan 14:12:25 (atau sekitar 14,206944 jam).

Untuk melihat seberapa baik model tersebut, kita dapat melihat selisih antara nilai yang diperoleh dari situs web tersebut dan nilai yang dihasilkan oleh model kita. Selisih tersebut sering disebut dengan galat.

Galat pada 31-12-2025: ${\text{14,208333}-L\left( {1096} \right)} \approx -\text{0,006267}$

Galat pada 31-12-2045: ${\text{14,206944}-L\left( {8401} \right)} \approx \text{0,197496}$

Berdasarkan hal tersebut, kita dapat menduga bahwa model kita akan semakin berkurang akurasinya ketika waktunya semakin jauh dari acuannya, yaitu 31-12-2022. Kita menduga demikian karena nilai mutlak galat pada 31-12-2045 lebih besar daripada 31-12-2025.

Kita selanjutnya dapat mengajukan pertanyaan-pertanyaan yang dapat memantik pemikiran kritis dan pemecahan masalah peserta didik: “Apakah betul demikian? Jika iya, bagaimana kamu dapat memperbaiki model tersebut?” Untuk memandu peserta didik agar dapat menjawab pertanyaan-pertanyaan tersebut, kita dapat memberikan data galat setiap 31 Desember mulai 2023 sampai 2045. Data tersebut dapat diakses melalui media pembelajaran yang beralamatkan di https://www.desmos.com/calculator/z2vmxjkk9b.

Melalui media pembelajaran tersebut, peserta didik dapat melihat tren galat yang dihasilkan oleh model L setiap waktunya. Tren galat tersebut disajikan pada Gambar 21 berikut.

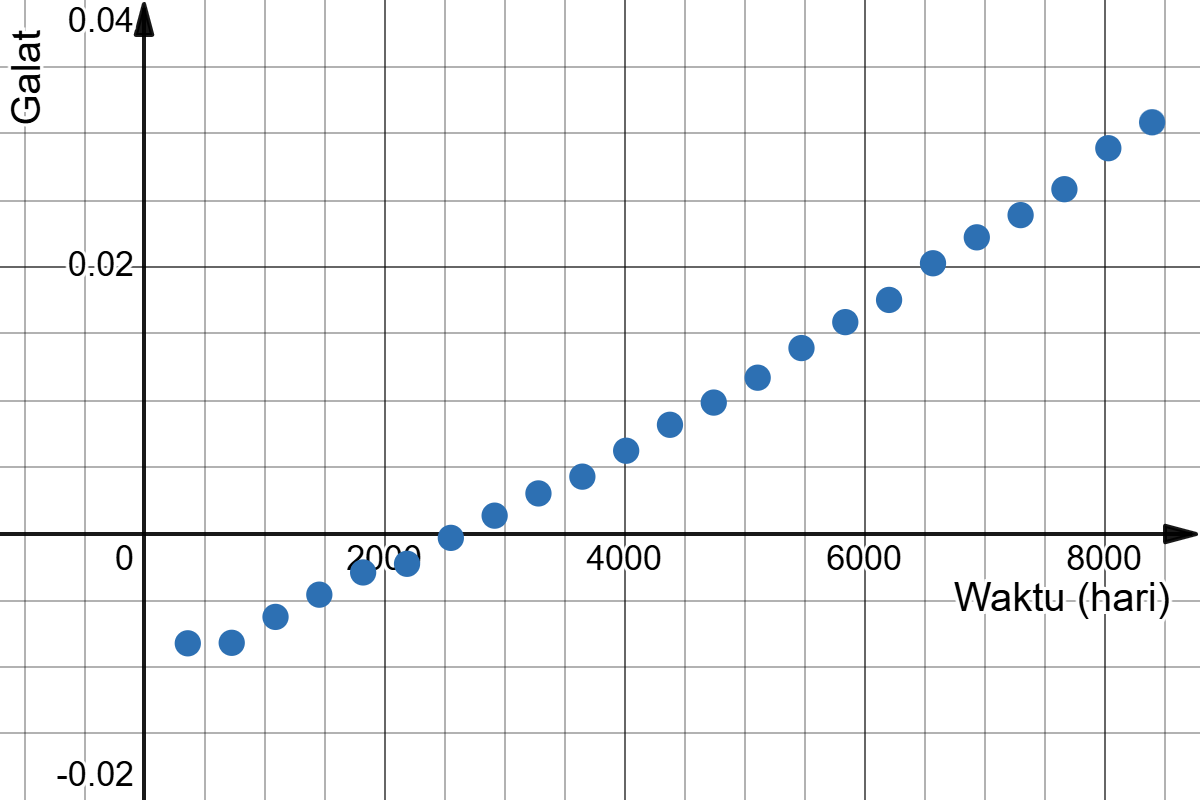
Grafik yang menunjukkan hubungan antara waktu (dalam hari) dan galat model untuk lamanya siang hari di Perth. Sumbu vertikal menunjukkan galat dalam jam, sementara sumbu horizontal menunjukkan waktu dalam hari. — Gambar 21. Tren galat yang dihasilkan oleh model L pada 31 Desember mulai 2023 sampai 2045

Peserta didik dapat menggunakan Gambar 21 tersebut sebagai bukti bahwa model L tersebut semakin lama semakin berkurang akurasinya. Melalui media pembelajaran yang disedikan, mereka juga dapat melihat seberapa akurat model tersebut dengan menggunakan nilai akar dari rerata kuadrat galatnya atau RMSE. Semakin kecil RMSE-nya, semakin akurat modelnya. Nilai RMSE untuk model L adalah sekitar 0,015108.

Untuk memandu peserta didik memperbaiki model L tersebut, kita dapat meminta mereka memikirkan kembali periode modelnya. Periode model L adalah 365, yang merupakan banyaknya hari dalam setahun. Namun, apakah betul bahwa banyaknya hari dalam setahun adalah 365? Bagaimana dengan tahun kabisat?

Banyaknya hari pada tahun kabisat adalah 366. Tahun kabisat tersebut terjadi setiap empat tahun sekali. Dengan demikian, secara rata-rata banyaknya hari dalam setahun adalah 365,25. Dengan informasi ini, kita dapat meminta peserta didik untuk memperbaiki modelnya menjadi seperti berikut. Model tersebut memiliki periode 365,25.

$\displaystyle L\left( x \right)=\text{2,094725}\cos \left[ {\frac{{2\pi }}{{\text{365,25}}}\left( {x-356} \right)} \right]+\text{12,150835}$

Berdasarkan model yang baru tersebut, kita mendapatkan RMSE yang lebih kecil, yaitu sekitar 0,010015. Akan tetapi, model yang baru tersebut menyebabkan semua galatnya negatif. Berdasarkan hal ini, kita dapat meminta peserta didik untuk menemukan penyebabnya dan bagaimana cara memperbaikinya lagi.

Sekarang beralih ke permasalahan Teluk Kupang. Dalam menganalisis grafik yang disebutkan dalam permasalahan ini, lihat kembali Gambar 7, peserta didik diharapkan dapat menemukan bahwa amplitudo grafiknya adalah 0,4 dan periodenya adalah 12. Dengan demikian, fungsi yang memodelkan ketinggian air Teluk Kupang setiap waktunya adalah $\displaystyle y=\text{0,4}\sin \left( {\tfrac{\pi }{6}x} \right)$ . Alhasil, ketinggian air (dalam m) tersebut pada pukul 16:00 dapat ditentukan seperti berikut.

$\displaystyle y=\text{0}\text{,4}\sin \left( {\frac{\pi }{6}\cdot 16} \right)\approx \text{0}\text{,35}$

Ringkasnya, pemahaman tentang grafik fungsi trigonometri memberikan ruang yang lebih luas bagi peserta didik untuk mendeskripsikan, memprediksi, dan mengomunikasikan fenomena-fenomena di sekitar mereka. Dengan ilustrasi variasi lamanya siang hari di Perth dan pasang surut Teluk Kupang sebelumnya, grafik fungsi trigonometri dapat digunakan oleh peserta didik untuk memahami fenomena-fenomena di sekitarnya.

Identitas Trigonometri

Salah satu karakteristik mata pelajaran matematika tingkat lanjut adalah mengajak peserta didik untuk bernalar dan membuktikan kebenaran suatu prinsip, rumus, atau teorema tertentu. Proses seperti ini betul-betul kami fasilitasi dalam kegiatan pembelajaran yang akan dialami peserta didik berikutnya, yaitu identitas trigonometri. Pada topik ini, peserta didik diharapkan mampu menggunakan identitas-identitas trigonometri dasar untuk membuktikan identitas-identitas trigonometri lainnya.

Berdasarkan tujuan seperti itu, pertama kami mengajak peserta didik bernalar untuk menemukan salah satu identitas trigonometri dasar, yaitu sin² t + cos² t = 1, dengan menggunakan lingkaran satuan. Selanjutnya, kami mengenalkan beberapa identitas trigonometri dasar lainnya, yaitu identitas kebalikan ( $\csc t={1}/{{\sin t}}\;$ , $\sec t={1}/{{\cos t}}\;$ , dan $\cot t={1}/{{\tan t}}\;$ ), hasil bagi ( $\tan t={{\sin t}}/{{\cos t}}\;$ dan $\cot t={{\cos t}}/{{\sin t}}\;$ ), Pythagoras ( ${{\sin }^{2}}t+{{\cos }^{2}}t=1$ , ${{\tan }^{2}}t+1={{\sec }^{2}}t$ , dan $1+{{\cot }^{2}}t={{\csc }^{2}}t$ ), dan genap-ganjil ( $\sin \left( {-t} \right)=-\sin t$ , $\cos \left( {-t} \right)=\cos t$ , dan $\tan \left( {-t} \right)=-\tan t$ ).

Identitas-identitas trigonometri dasar tersebut menjadi modal peserta didik untuk membuktikan dan menemukan identitas trigonometri lainnya. Selanjutnya, kami memberikan contoh bagaimana metode membuktikan sebuah identitas trigonometri. Identitas tersebut adalah sebagai berikut.

$\displaystyle \frac{{\cos t+1}}{{{{{\tan }}^{2}}t}}=\frac{{\cos t}}{{\sec t-1}}$

Pembuktian identitas tersebut dapat dilakukan dengan berbagai cara. Cara pertama, kita dapat memanipulasi bentuk di ruas kiri untuk menunjukkan bahwa bentuk ini sama dengan yang di ruas kanan. Cara kedua adalah kebalikan cara pertama. Kita dapat memanipulasi bentuk di ruas kanan untuk menunjukkan bahwa bentuk ini sama dengan yang di ruas kiri. Terakhir, kita dapat memanipuasi bentuk di ruas kiri maupun kanan ke dalam bentuk-bentuk tertentu dan menunjukkan bentuk-bentuk tersebut sama.

Misalnya, kita dapat menggunakan cara kedua untuk membuktikan identitas tersebut.

$\displaystyle \frac{{\cos t}}{{\sec t-1}}$

$\displaystyle =\frac{{\cos t}}{{\sec t-1}}\cdot \frac{{\sec t+1}}{{\sec t+1}}$

Kalikan dengan 1 dalam bentuk $\frac{{\sec t+1}}{{\sec t+1}}$

$\displaystyle =\frac{{\cos t\left( {\sec t+1} \right)}}{{{{{\sec }}^{2}}t-1}}$

Perkalian sekawan

$\displaystyle =\frac{{\cos t\left( {\frac{1}{{\cos t}}+1} \right)}}{{{{{\tan }}^{2}}t}}$

Identitas kebalikan dan Pythagoras

$\displaystyle =\frac{{1+\cos t}}{{{{{\tan }}^{2}}t}}=\frac{{\cos t+1}}{{{{{\tan }}^{2}}t}}$

Sederhanakan

Pemberian contoh pembuktian identitas trigonometri tersebut penting bagi peserta didik karena beberapa alasan. Pertama, contoh tersebut memberikan ilustrasi proses matematis yang perlu dilakukan oleh peserta didik untuk membuktikan sebuah identitas trigonometri. Hal ini akan memberikan panduan bagi peserta didik untuk membuktikan identitas-identitas lainnya. Kedua, contoh tersebut memberikan model pembuktian identitas trigonometri yang valid. Hal ini dimaksudkan untuk mencegah kekeliruan peserta didik dalam membuktikan identitas trigonometri. Salah satu kemungkinan kekeliruan tersebut adalah sebagai berikut.

$\displaystyle \frac{{\cos t+1}}{{{{{\tan }}^{2}}t}}$

$\displaystyle =\frac{{\cos t}}{{\sec t-1}}$

$\displaystyle \frac{{\cos t+1}}{{{{{\sec }}^{2}}t-1}}$

$\displaystyle =\frac{{\cos t}}{{\sec t-1}}\cdot \frac{{\sec t+1}}{{\sec t+1}}$

$\displaystyle \frac{{\cos t+1}}{{{{{\sec }}^{2}}t-1}}$

$\displaystyle =\frac{{\cos t\left( {\frac{1}{{\cos t}}+1} \right)}}{{{{{\sec }}^{2}}t-1}}$

$\displaystyle \frac{{\cos t+1}}{{{{{\sec }}^{2}}t-1}}$

$\displaystyle =\frac{{\cos t+1}}{{{{{\sec }}^{2}}t-1}}$

Cara di atas keliru karena langkah/baris pertama telah menggunakan persamaan $\frac{{\cos t+1}}{{{{{\tan }}^{2}}t}}=\frac{{\cos t}}{{\sec t-1}}$ . Artinya, persamaan tersebut diasumsikan benar untuk sembarang t yang membuat bentuk di kedua ruas terdefinisi. Padahal asumsi itulah yang akan dibuktikan kebenarannya.

Kami juga mengenalkan metode untuk melakukan pengujian awal apakah sebuah persamaan merupakan identitas trigonometri. Metode ini menggunakan kalkulator grafik. Misalnya, sebelum membuktikan identitas trigonometri sebelumnya, peserta didik dapat menyelidiki apakah kedua fungsi berikut sama melalui pengamatan grafiknya.

$\displaystyle y=\frac{{\cos t+1}}{{{{{\tan }}^{2}}1}}$

$\displaystyle y=\frac{{\cos t}}{{\sec t-1}}$

Untuk melakukannya peserta didik dapat menginputkan kedua fungsi tersebut ke dalam kalkulator grafik untuk diamati grafiknya. Tangkapan layar kalkulator grafik yang menunjukkan grafik kedua fungsi tersebut ditampilkan pada Gambar 22.

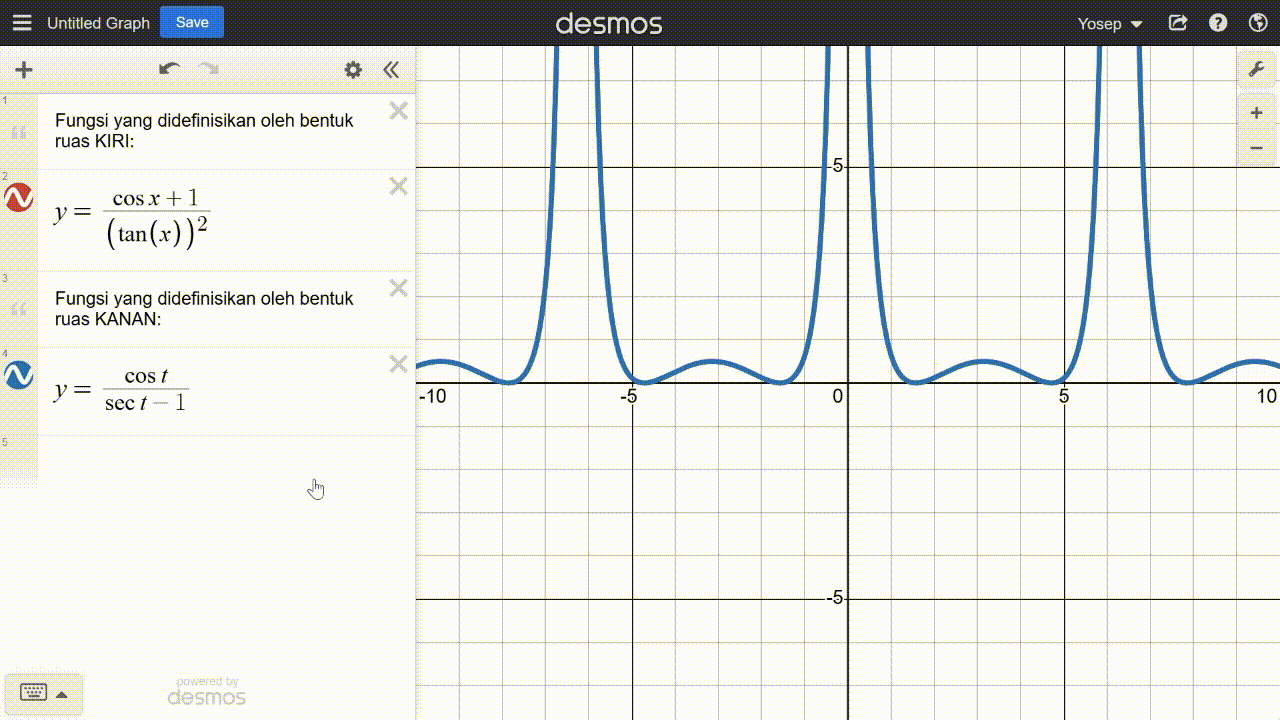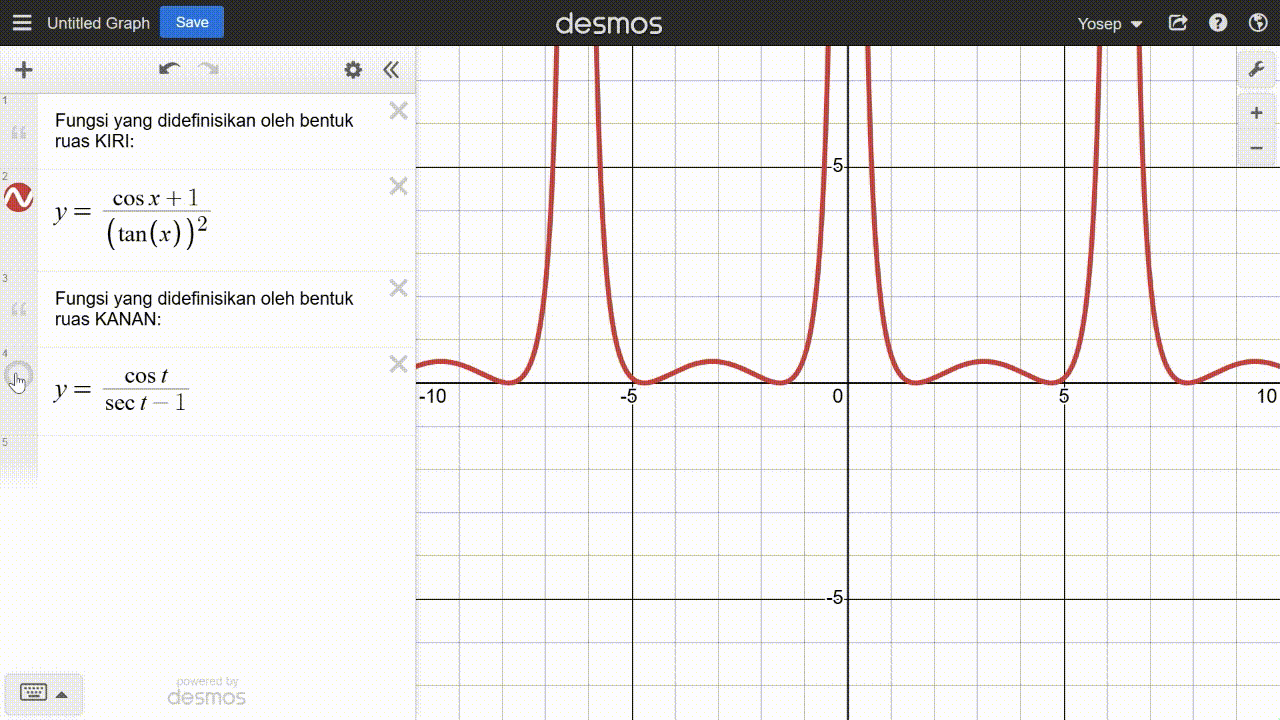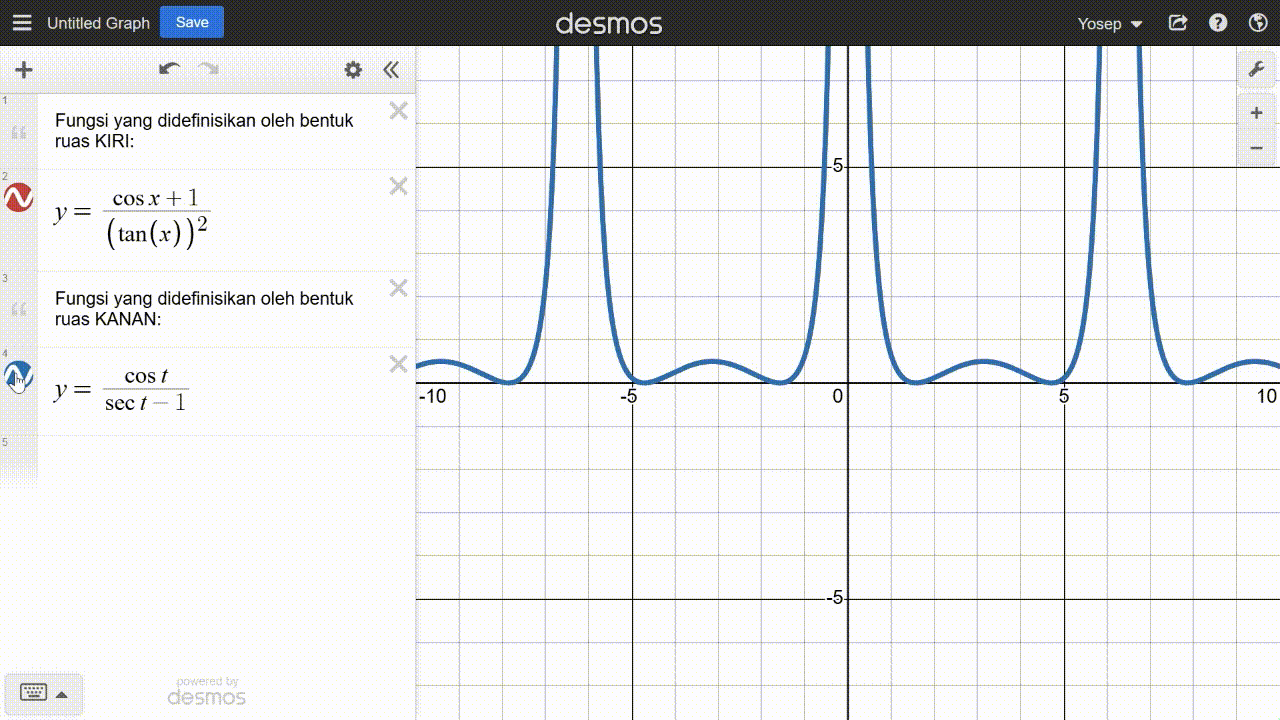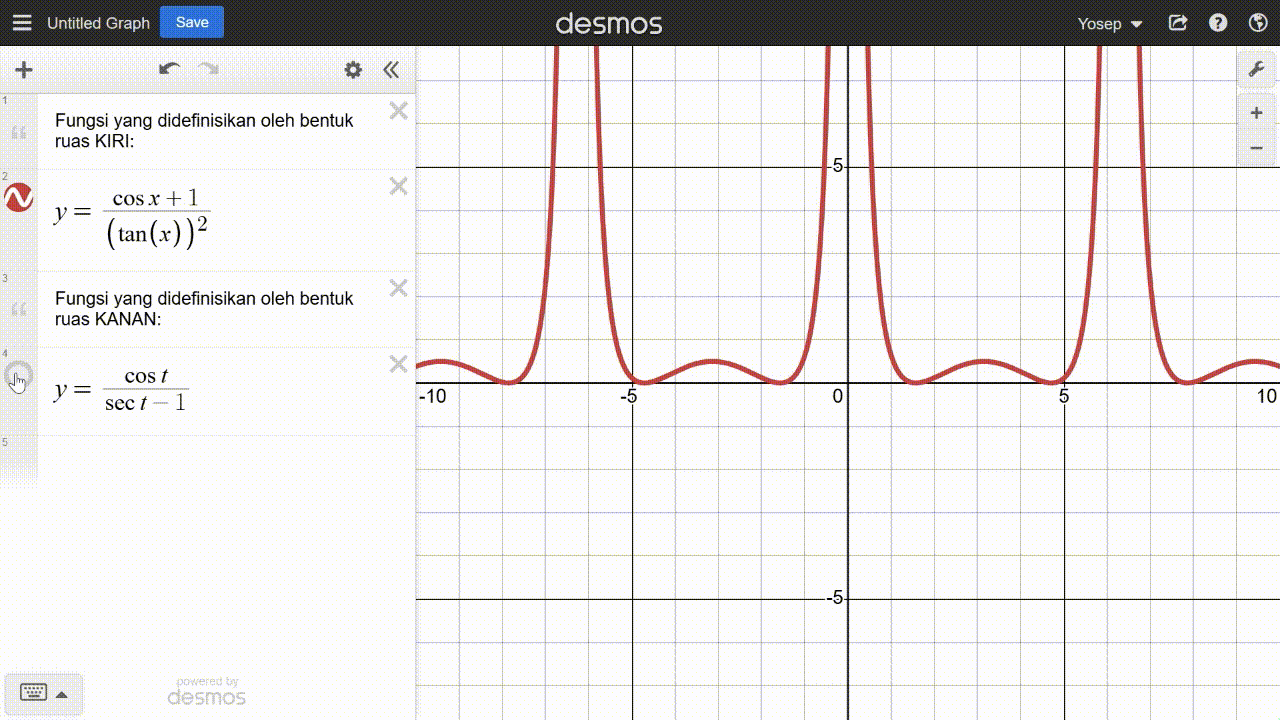
Gambar 22. Tangkapan layar kalkulator grafik

Berdasarkan Gambar 22, peserta didik diharapkan dapat mengamati bahwa grafik kedua fungsi tersebut berimpit pada jendela kalkulator tersebut. Dengan demikian, hal itu menjadi bukti awal bahwa kedua fungsi tersebut sama (paling tidak untuk setiap x pada jendela kalkulator tersebut, yaitu mulai dari –10 sampai 10). Dengan modal ini, peserta didik memiliki pertimbangan tentang strategi mereka selanjutnya dalam membuktikan identitas trigonometri yang diberikan.

Sebagai catatan penting, metode membandingkan grafik tersebut bukanlah metode untuk membuktikan identitas trigonometri. Akan tetapi, metode tersebut sangat berguna sebagai penyelidikan awal untuk mengetahui apakah persamaan yang diberikan merupakan identitas trigonometri. Pembuktian identitas trigonometri dilakukan seperti yang dicontohkan dan dipaparkan sebelumnya.

Untuk membuat repertoar peserta didik tentang identitas trigonometri lebih kaya, selanjutnya kami memandu peserta didik untuk menemukan identitas penjumlahan dan pengurangan sudut untuk kosinus melalui aktivitas pembelajaran eksploratif. Identitas tersebut adalah $\cos \left( {A+B} \right)=\cos A\cos B-\sin A\sin B$ dan $\displaystyle \cos \left( {A-B} \right)=\cos A\cos B+\sin A\sin B$ .

Kedua identitas tersebut sangat penting untuk membuktikan identitas-identitas trigonometri lainnya. Identitas-identitas tersebut di antaranya adalah identitas trigonometri yang mengoneksikan fungsi sinus dan kosinus: $\displaystyle \cos \left( {\frac{\pi }{2}-x} \right)=\sin x$ dan $\displaystyle \sin \left( {\frac{\pi }{2}-x} \right)=\cos x$ . Repertoar identitas-identitas trigonometri tersebut selanjutnya dapat digunakan untuk membuktikan identitas penjumlahan dan pengurangan sudut untuk sinus: $\displaystyle \sin \left( {A+B} \right)=\sin A\cos B+\cos A\sin B$ dan $\sin \left( {A-B} \right)=\sin A\cos B-\cos A\sin B$ .

Pembelajaran pada topik identitas trigonometri ini memberi kesempatan kepada peserta didik untuk bernalar dan membuktikan identitas-identitas trigonometri. Alur pembelajaran dalam topik tersebut kami susun sekoheren mungkin sehingga apa yang peserta didik temukan atau buktikan menjadi dasar proses penemuan dan pembuktian selanjutnya.

Aturan Sinus

Salah satu khasiat penting trigonometri adalah untuk menyelesaikan permasalahan geometris yang melibatkan segitiga. Tak hanya eksklusif untuk segitiga siku-siku, trigonometri juga dapat digunakan untuk segitiga sembarang! Untuk dapat menggunakan potensi ini, peserta didik perlu memahami Aturan Sinus, salah satunya, dan menerapkan aturan tersebut untuk menyelesaikan berbagai macam permasalahan.

Untuk mencapai tujuan tersebut, kami memfasilitasi peserta didik untuk menemukan Aturan Sinus melalui aktivitas pembelajaran eksploratif. Di akhir aktivitas pembelajaran tersebut, mereka menemukan bahwa untuk sembarang segitiga ABC yang panjang sisi-sisinya a, b, dan c, persamaan berikut selalu benar.

$\displaystyle \frac{{\sin A}}{a}=\frac{{\sin B}}{b}=\frac{{\sin C}}{c}$

Persamaan itulah yang disebut dengan Aturan Sinus. Setelah itu, kami memberikan kesempatan bagi peserta didik untuk menerapkan aturan tersebut dalam menyelesaikan permasalahan matematis maupun masalah sehari-hari yang melibatkan segitiga.

Kami juga tak lupa akan “kasus-kasus ambigu” dalam penerapan Aturan Sinus tersebut. Kasus ambigu tersebut merujuk pada kasus yang dapat menghasilkan tepat satu selesaian, dua selesaian, atau tanpa selesaian. Untuk mengenalkan kasus ambigu tersebut, kami tidak langsung memberikannya kepada peserta didik. Melainkan, kami mengajak peserta didik untuk berpikir kritis dalam menganalisis dan mengevaluasi strategi orang lain dalam menyelesaikan permasalahan segitiga. Perhatikan permasalahan berikut.

Paulina menyelesaikan soal berikut.
Diberikan sebuah segitiga ABC dengan ∠A = 45°, a = 7, dan b = 12.
Pengerjaan Paulina ditunjukkan pada Gambar 23 berikut.

Pada hasil akhir pekerjaannya, dia mendapatkan sin B ≈ 1,21. Dia mengetahui bahwa nilai maksimum sinus adalah 1 sehingga dia bingung apakah perhitungannya salah atau ada alasan lain. Bantulah Paulina menyelesaikan kebingungannya!

Permasalahan tersebut memantik peserta didik untuk menemukan bahwa tidak mungkin terdapat sebuah segitiga ABC dengan ∠A = 45°, a = 7, dan b = 12. Hal ini diilustrasikan oleh animasi pada Gambar 24 berikut.

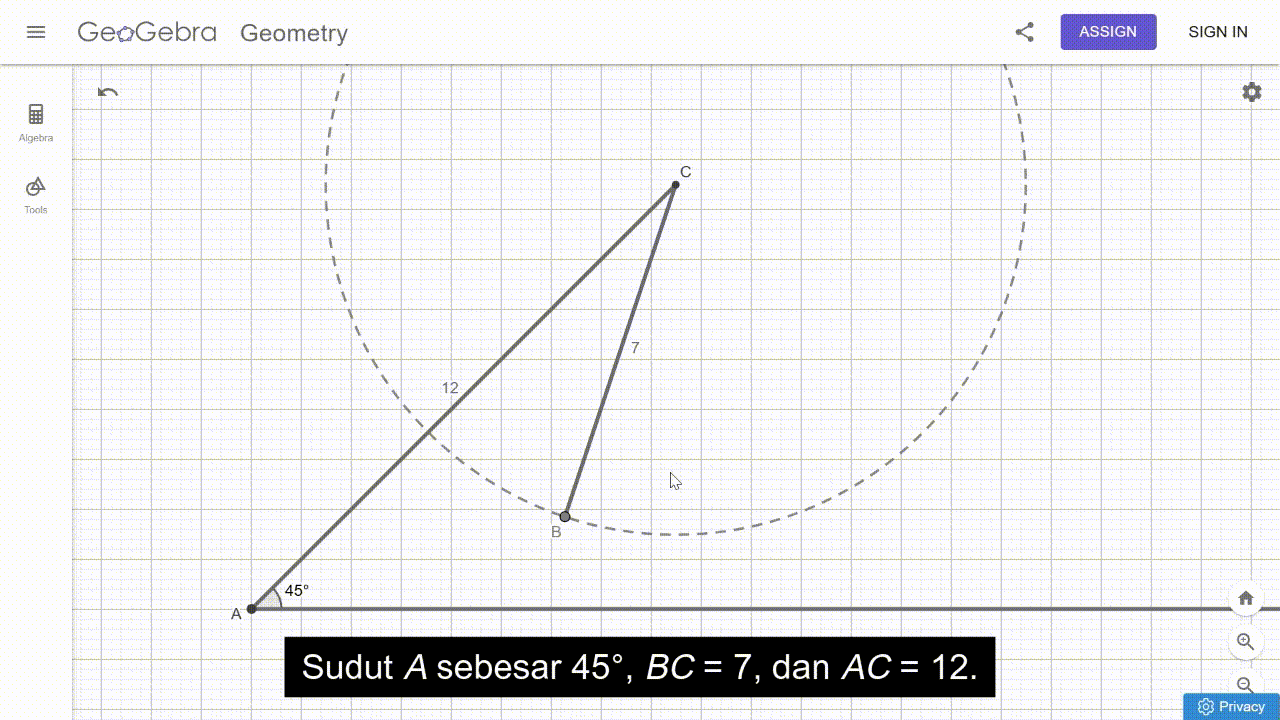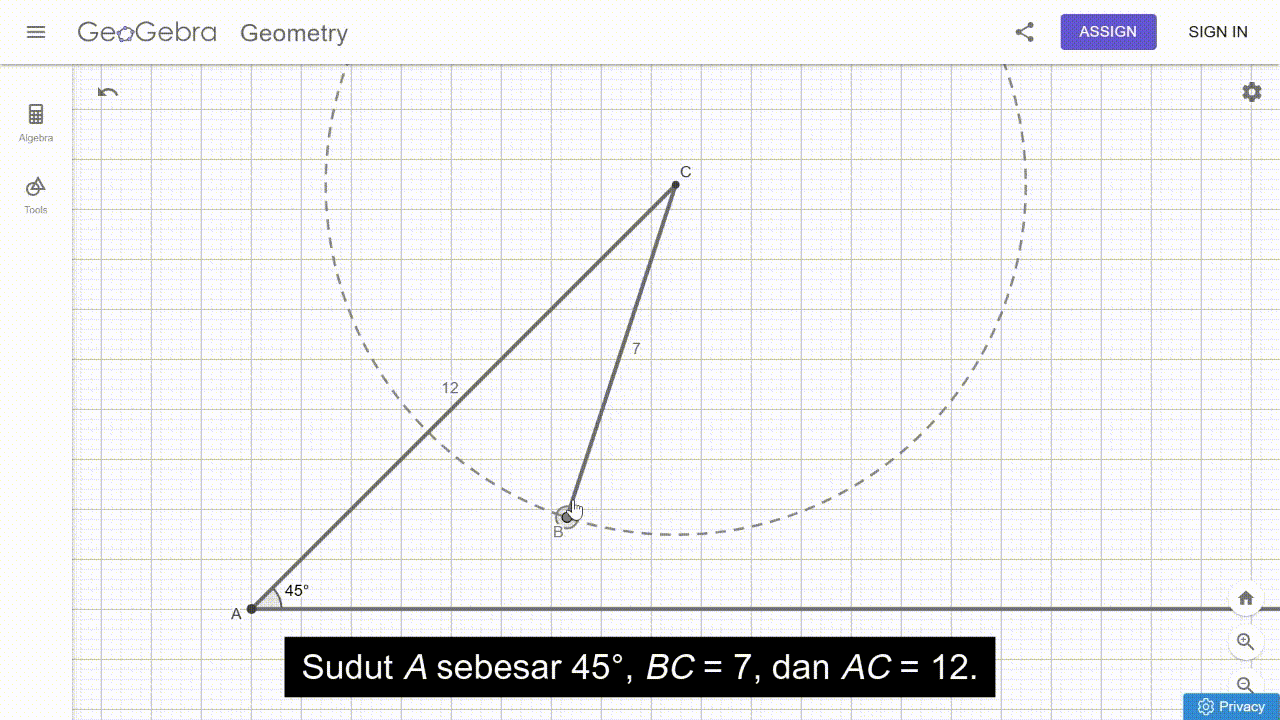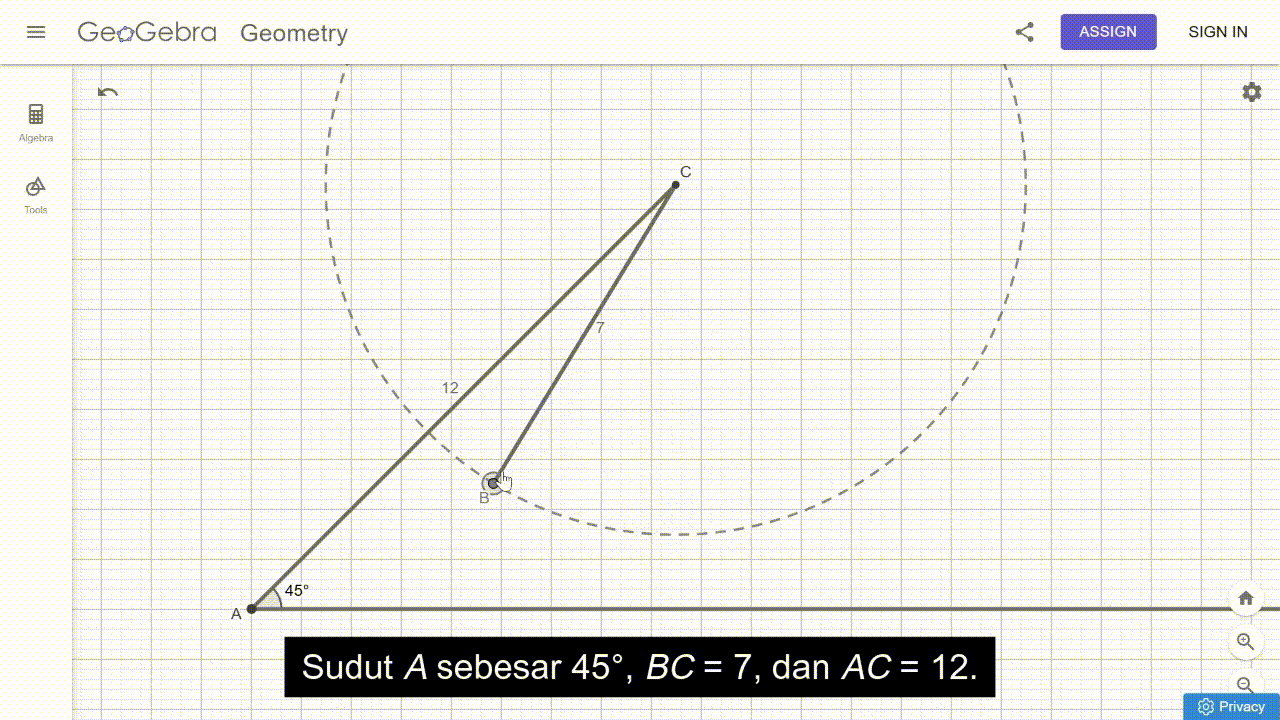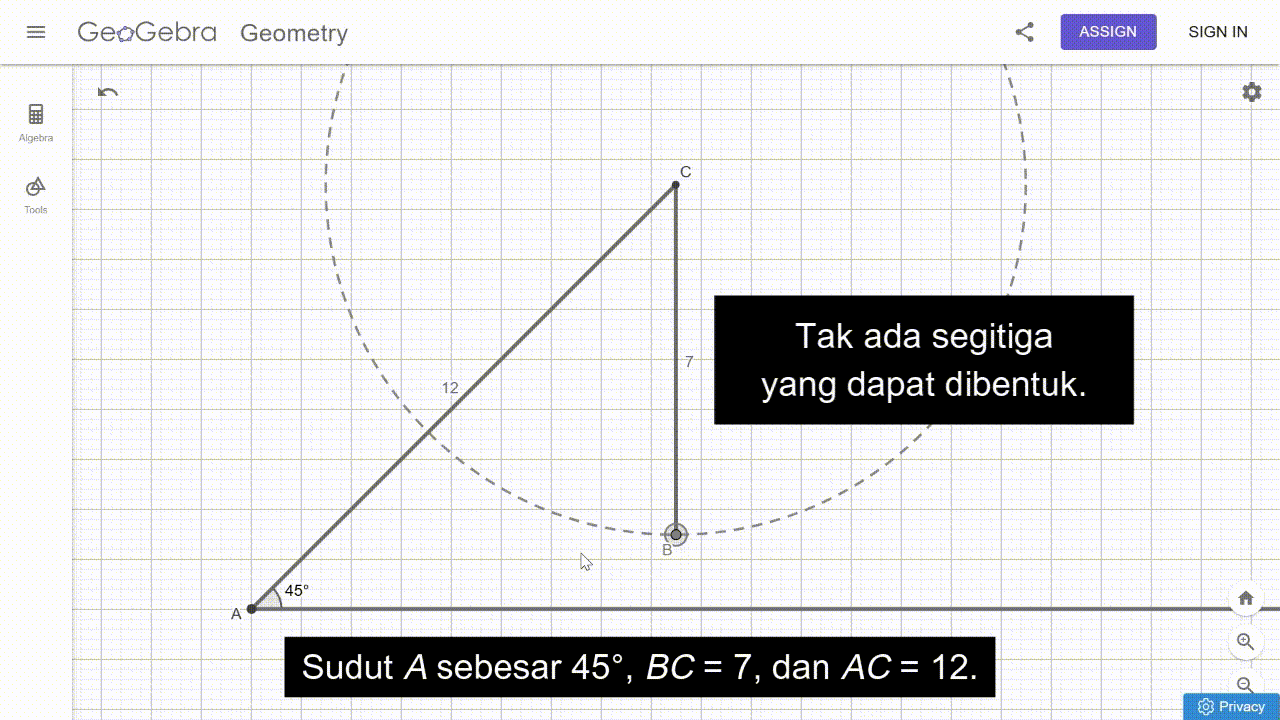
Gambar 24. Ilustrasi salah satu kasus tanpa selesaian

Berdasarkan temuan tersebut, kita dapat memberikan pertanyaan lebih lanjut kepada peserta didik untuk memantik pemikiran kritisnya. Misalnya, “Informasi apa yang perlu diubah agar kamu mendapatkan minimal satu segitiga? Informasi tersebut perlu diubah menjadi seperti apa?” Pertanyaan-pertanyaan ini akan memantik peserta didik untuk bereksplorasi. Mereka mungkin akan menemukan jawaban seperti berikut.

Mereka perlu memperkecil besar sudut A sehingga besarnya di antara 0° dan 35,68°.
Mereka perlu memperpanjang sisi BC agar panjangnya setidaknya $6\sqrt{2}$ atau sekitar 8,49.
Mereka perlu membuat sisi AC lebih pendek menjadi kurang dari atau sama dengan $7\sqrt{2}$ atau sekitar 9,89.

Menyelam Lebih Dalam: Mengurai Kasus Ambigu

Kita dapat memfasilitasi peserta didik untuk melakukan aktivitas pembelajaran eksploratif terkait dengan kasus ambigu tersebut secara lebih mendalam. Pada permasalahan sebelumnya, kasus ambigu terjadi ketika diberikan sebuah segitiga yang diketahui panjang kedua sisinya dan besar satu sudut di hadapan salah satu sisi tersebut. Kasus ini sering disebut dengan sisi-sisi-sudut.

Kita dapat memandu peserta didik untuk mengeksplorasi kemungkinan-kemungkinan lain kasus sisi-sisi-sudut tersebut. Misalnya, kita dapat menggunakan media pembelajaran digital yang telah kami kembangkan dengan GeoGebra. Media pembelajaran tersebut dapat diakses di https://www.geogebra.org/classic/dvxdqh7t. Gambar 25 menunjukkan tangkapan layar media pembelajaran tersebut.

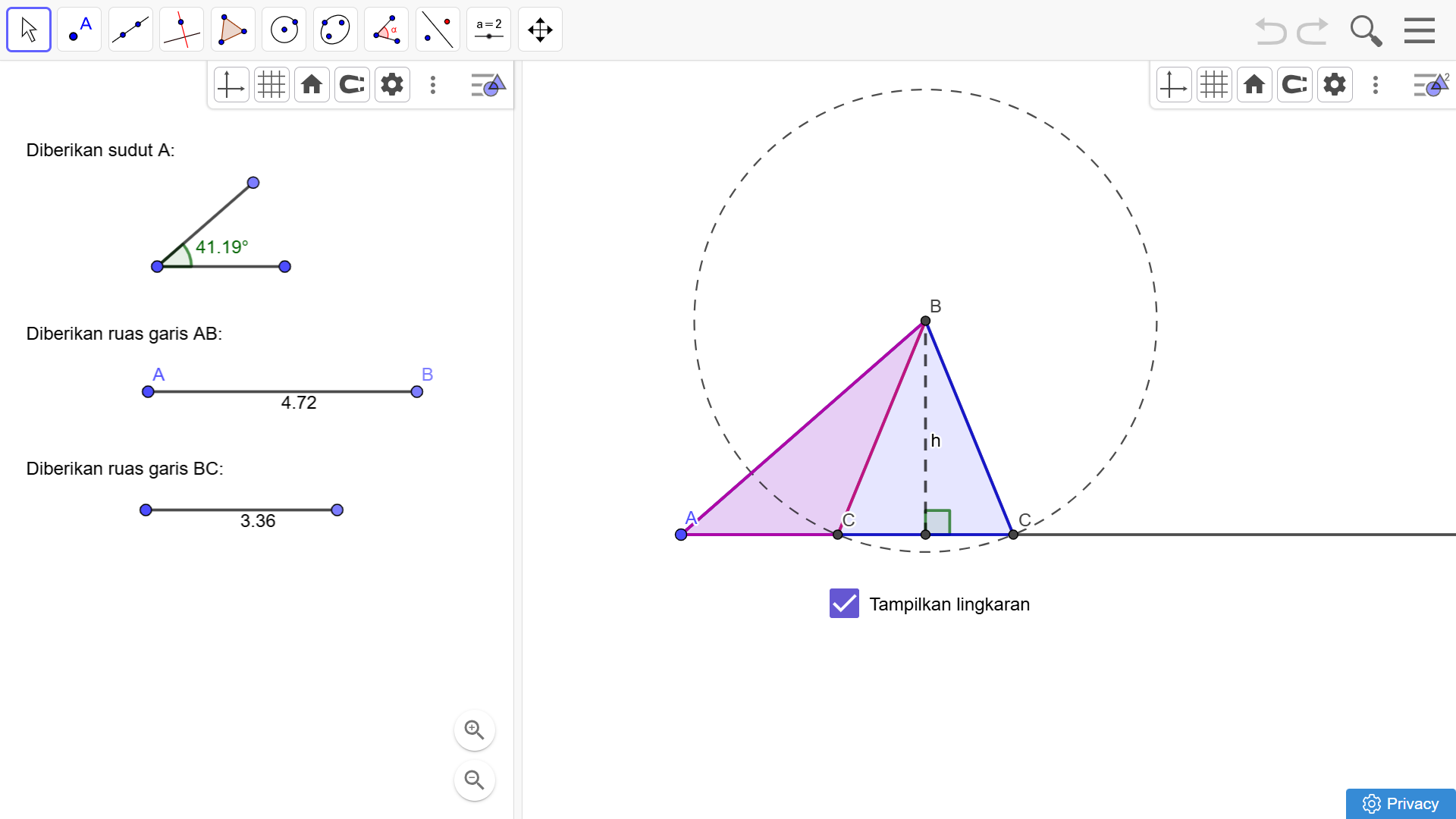
Gambar 25. Eksplorasi kasus ambigu sisi-sisi-sudut

Melalui media pembelajaran tersebut, peserta didik dapat mengubah-ubah ukuran sudut dalam A, serta panjang ruas garis AB dan BC. Untuk dapat memanfaatkannya, mereka dapat dipandu dengan menggunakan pertanyaan pemantik berikut: “Untuk kasus sisi-sisi-sudut, kapan kita mendapatkan tepat satu segitiga? Dua segitiga? Tidak mendapatkan segitiga?”

Dalam menjawab pertanyaan-pertanyaan tersebut, misalnya, peserta didik dapat dipandu untuk mengurai permasalahan tersebut menjadi tiga kasus berdasarkan besar sudut A: (a) sudut A adalah sudut lancip; (b) sudut A adalah sudut siku-siku; dan (c) sudut A adalah sudut tumpul. Dengan cara seperti ini, mereka akan dapat lebih berfokus dalam menjawab pertanyaan-pertanyaan awal tersebut di setiap kasusnya.

Misalnya, ketika mereka memerhatikan kasus pertama (sudut A adalah sudut lancip), mereka akan mendapati bahwa ketika panjang sisi BC kurang dari panjang garis tinggi di hadapan sudut A (misalkan h), maka tidak ada segitiga yang terbentuk. Hal ini adalah keadaan seperti pada permasalahan Paulina sebelumnya, lihat kembali Gambar 22. Mereka dapat mengeksplorasi keadaan-keadaan lain di setiap kasusnya dan mencatat hasilnya. Hasil tersebut dapat dicatat menggunakan templat seperti Tabel 1 berikut.

Banyak Segitiga	Sudut A Lancip	Sudut A Siku-Siku	Sudut A Tumpul
0	BC < h
1
2

Tabel 1. Contoh templat pencatatan hasil eksplorasi kasus ambigu sisi-sisi-sudut

Aturan Sinus membuka kemungkinan bagi peserta didik untuk menyelesaikan berbagai permasalahan tentang segitiga. Akan tetapi, aturan tersebut tidak dapat digunakan untuk menyelesaikan segitiga yang diketahui panjang dua sisi dan besar satu sudut yang diapit kedua sisi tersebut (sisi-sudut-sisi) dan segitiga yang diberikan panjang ketiga sisinya (sisi-sisi-sisi). Kedua kasus ini dapat diselesaikan dengan menggunakan aturan lainnya, yaitu Aturan Kosinus.

Aturan Kosinus

Topik terakhir dalam alur pembelajaran pada fungsi trigonometri adalah Aturan Kosinus. Aturan Kosinus ini melengkapi Aturan Sinus untuk menyelesaikan permasalahan segitiga. Alur pembelajaran Aturan Kosinus ini serupa dengan alur pembelajaran pada Aturan Sinus. Pertama, peserta didik diminta untuk menemukan Aturan Kosinus melalui kegiatan eksploratif. Kegiatan pembelajaran tersebut dipandu oleh permasalahan sebagai berikut.

Misalkan kita memiliki segitiga ABC yang panjang sisi-sisinya a, b, dan c, dengan A di titik asal O(0, 0) dan B pada sumbu-x positif.

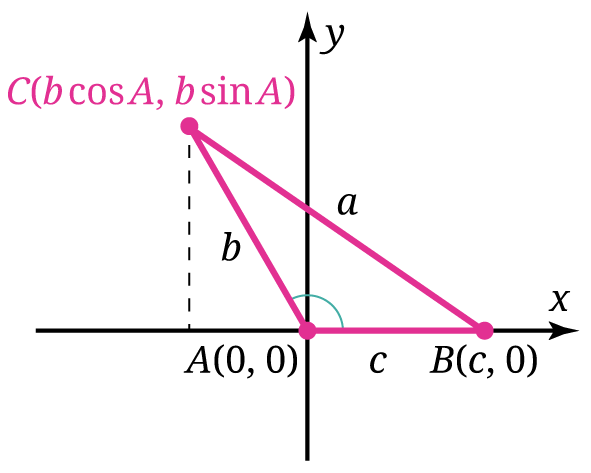
Gambar 26. Segitiga *ABC* pada bidang koordinat

Berdasarkan informasi dan Gambar 26, jawablah pertanyaan berikut.

Mengapa koordinat titik C adalah (b cos A, b sin A). Apakah koordinatnya tetap meskipun sudut A lancip?
Tentukan panjang BC menggunakan rumus jarak (teorema Pythagoras).
Karena BC = a, berdasarkan hasil dari nomor 2, apakah kamu dapat menunjukkan bahwa a² = b² + c² – 2bc cos A?

Setelah peserta didik menyelesaikan kegiatan eksploratif tersebut, mereka diberikan istilah “Aturan Kosinus” untuk persamaan yang baru mereka temukan. Selain itu, mereka juga diberikan beberapa variasi persamaan dalam Aturan Kosinus, yaitu seperti berikut.

$\displaystyle {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A$

$\displaystyle {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cos B$

$\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos C$

Selanjutnya, mereka diberi kesempatan untuk menerapkan aturan tersebut untuk menyelesaikan berbagai macam permasalahan, baik untuk kasus sisi-sudut-sisi maupun sisi-sisi-sisi. Di akhir topik Aturan Kosinus ini, peserta didik diharapkan memiliki pengetahuan dan keterampilan untuk menyelesaikan berbagai permasalahan yang melibatkan segitiga.

Catatan Penutup

Alur pembelajaran fungsi trigonometri yang kami usulkan tujuan utamanya adalah untuk membantu peserta didik mencapai capaian pembelajaran tentang topik tersebut pada fase F+. Pengalaman belajar pada subbab Fungsi Trigonometri dan Lingkaran Satuan memfasilitasi peserta didik untuk mampu menyatakan fungsi trigonometri menggunakan lingkaran satuan. Mereka belajar memodelkan fenomena periodik dengan menggunakan fungsi trigonometri dan grafiknya pada subbab Grafik Fungsi Trigonometri. Mereka juga membangun penalarannya dan berlatih untuk membuktikan berbagai macam identitas trigonometri pada subbab Identitas Trigonometri. Terakhir, mereka menerapkan Aturan Sinus dan Kosinus untuk menyelesaikan berbagai permasalahan yang melibatkan segitiga pada subbab Aturan Sinus dan Aturan Kosinus. Singkatnya, alur pembelajaran tersebut konsisten dengan mandat capaian pembelajaran.

Alur pembelajaran tersebut juga disusun sekoheren mungkin. Kegiatan-kegiatan pembelajarannya terurut secara logis sehingga kegiatan yang lebih dahulu membangun kegiatan-kegiatan berikutnya. Tak hanya itu, pembahasan konten matematikanya juga atas pertimbangan kemampuan awal peserta didik, khususnya tentang perbandingan trigonometri segitiga siku-siku. Kemendalaman materinya juga disusun berdasarkan potensi manfaat fungsi trigonometri bagi peserta didik untuk mendeskripsikan, memprediksi, dan mengomunikasikan fenomena-fenomena di sekitarnya.

Satu hal yang penting diingat, alur pembelajaran tersebut hanyalah usulan dari kami. Kami menyadari, alur pembelajaran tersebut bukanlah satu jalan untuk semua peserta didik. Jika pembaca memiliki alternatif lain yang lebih sesuai dengan peserta didiknya, silakan bagikan di kolom komentar. Senang dengan alur pembelajaran yang kami usulkan? Silakan bagikan artikel ini!

Cerita Petualangan Fungsi Trigonometri

Fungsi Trigonometri dan Lingkaran Satuan

Grafik Fungsi Trigonometri

Identitas Trigonometri

Aturan Sinus

Aturan Kosinus

Catatan Penutup

Diterbitkan oleh Yosep Dwi Kristanto

Tinggalkan komentar Batalkan balasan

Fungsi Trigonometri dan Lingkaran Satuan

Grafik Fungsi Trigonometri

Identitas Trigonometri

Aturan Sinus

Aturan Kosinus

Catatan Penutup

Bagikan ini:

Terkait

Diterbitkan oleh Yosep Dwi Kristanto

Tinggalkan komentar Batalkan balasan