Bagaimana matematika dapat digunakan untuk memahami keanekaragaman hayati di Kepulauan Raja Ampat? Selain menjawab pertanyaan tersebut, artikel ini secara ringkas membahas pemodelan matematis dengan berbagai macam fungsi dan membandingkan model-model yang terbentuk.
Sudah menjadi rahasia umum bahwa Kepulauan Raja Ampat memiliki daya tarik karena pesona keindahan alamnya. Tapi tahukah kamu, kepulauan ini juga menyimpan keanekaragaman hayati yang begitu kaya? Tim peneliti dari Jerman, Australia, dan Indonesia pernah menyelidiki keanekararagaman hayati di kepulauan tersebut. Dalam salah satu risetnya, mereka melihat hubungan antara luas wilayah dan banyaknya spesies tanaman berkayu yang tersimpan dalam kepulauan tersebut. Tak hanya itu, mereka juga memodelkan hubungan tersebut dengan menggunakan beberapa fungsi matematika.
Untungnya, data yang mereka gunakan dalam riset tersebut tersedia secara publik di Biodiversity Data Journal. Oleh karena itu, kita dapat menganalisis ulang data tersebut! Kita dapat memodelkan keanekaragaman spesies tanaman berkayu yang hidup di beberapa pulau dalam Kepulauan Raja Ampat. Untuk melakukannya, kamu dapat bereksplorasi melalui aplikasi berbasis web “Jelajah Kepulauan Raja Ampat”. Aplikasi ini merupakan media pembelajaran penunjang untuk buku Matematika Tingkat Lanjut untuk SMA/MA Kelas XI (Edisi Revisi).
Visualisasi Data dan Model
Melalui aplikasi tersebut, kamu dapat memvisualisasikan data pada tiga macam tingkat analisis, yaitu pulau, transek, atau subtransek. Kamu juga dapat memilih berbagai macam fungsi matematika untuk memodelkan datanya. Fungsi-fungsi matematika yang tersedia adalah fungsi linear, pangkat, logaritma, eksponensial negatif, rasional, logistik, dan Weibull. Selain itu, kamu juga dapat memilih apakah variabel luas wilayahnya ditransformasi dengan logaritma.
Misalnya, kita pilih tingkat analisis pulau dan kita tidak mentransformasi variabel luas dalam data tersebut. Model linear dan fungsi rasional untuk data tersebut disajikan pada Gambar 1 berikut.
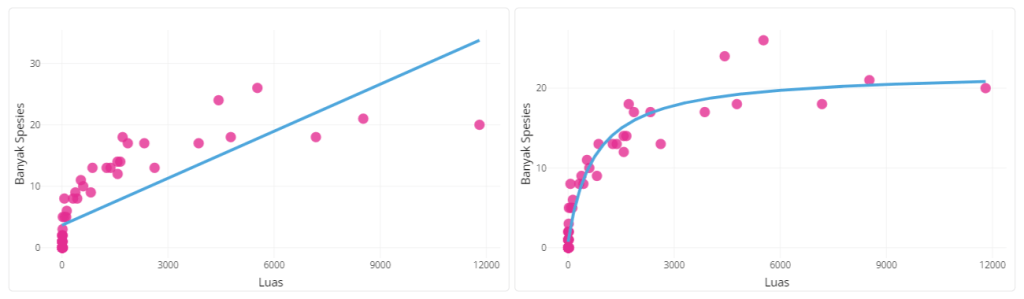
Pada Gambar 1, modelnya digambarkan dalam sebuah garis lurus (untuk fungsi linear) dan kurva (untuk fungsi rasional). Kedua model tersebut memiliki persamaan sebagai berikut.
dengan 
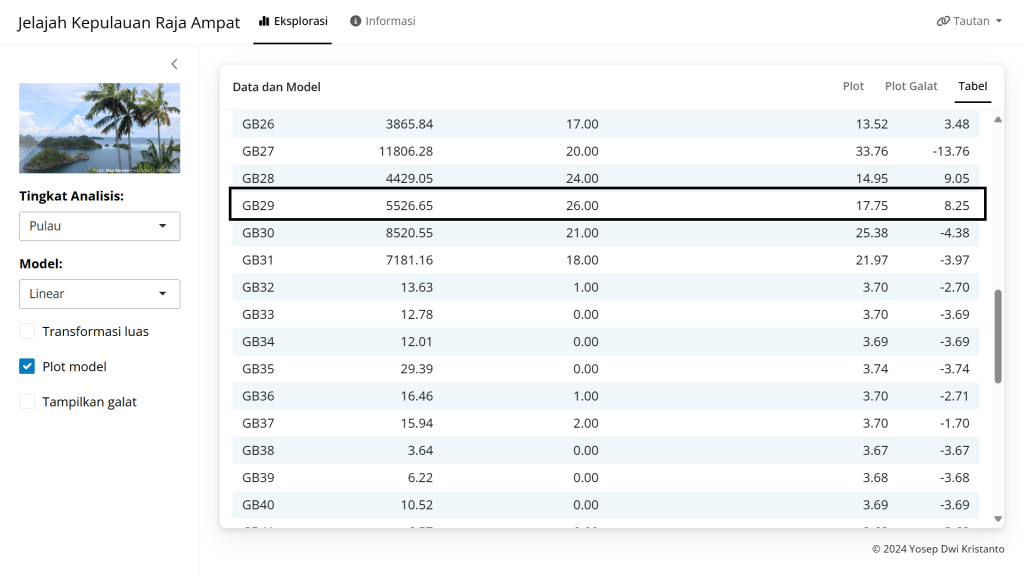
Faktanya, jika kamu melihat tabel datanya, lihat Gambar 2, pulau yang luasnya 5526,65 (yaitu pulau dengan ID GB29) dihuni oleh 26 spesies tanaman berkayu. Terdapat selisih antara banyak spesies sebenarnya dalam pulau tersebut dan banyak spesies yang diperoleh dari model. Selisih inilah yang disebut dengan galat.
Membandingkan Model
Kita telah memodelkan hubungan antara luas pulau dan banyaknya spesies tanaman berkayu dalam pulau tersebut dengan menggunakan fungsi linear dan rasional. Pertanyaan berikutnya, model mana yang lebih baik? Untuk menjawab pertanyaan ini, paling tidak kita dapat menggunakan dua cara, yaitu cara visual dan menggunakan galat-galatnya.
Cara visual dapat dilakukan hanya dengan melihat diagram pencarnya. Silakan lihat kembali Gambar 1. Dari gambar tersebut, menurutmu kurva mana yang lebih baik untuk meringkas pola datanya? Yup, kurva dari fungsi rasional tampak lebih baik untuk menggambarkan pola datanya.
Meskipun cara visual cenderung mudah dilakukan, tingkat akurasinya masih diragukan. Lebih jauh, kamu akan merasa kesulitan untuk membandingkan dua model yang sama-sama baik. Misalnya, silakan bandingkan model fungsi rasional dan Weibull! Lebih sukar, bukan?
Cara yang kedua adalah dengan menggunakan galat-galat modelnya. Model yang lebih baik memiliki galat-galat yang lebih dekat dengan nol. Untuk menggunakan cara ini, kamu dapat menggunakan jumlah kuadrat galat (SSE, sum of squares error) atau akar dari rerata kuadrat galat (RMSE, root mean squared error).
Untuk menghitung SSE maupun RMSE, kamu perlu memiliki data kuadrat dari galat. Untungnya, bagian Tabel di aplikasi Jelajah Kepulauan Raja Ampat sudah menyediakan kolom Galat. Kamu tinggal menambahkan satu kolom lagi yang isinya merupakan kuadrat dari galat untuk setiap barisnya. Tabel 1 berikut menyajikan tabel data untuk model linear yang sudah disertai dengan kolom kuadrat galat.
| ID Pulau | Luas | Banyak Spesies | Banyak Spesies (Pred. Model) | Galat | Kuadrat Galat |
|---|---|---|---|---|---|
| GB1 | 4774,04 | 18,00 | 15,83 | 2,17 | 4,7089 |
| GB2 | 7,29 | 1,00 | 3,68 | -2,68 | 7,1824 |
| GB3 | 2329,91 | 17,00 | 9,60 | 7,40 | 54,76 |
| … | … | … | … | … | … |
| GB58 | 16,77 | 0,00 | 3,71 | -3,71 | 13,7641 |
| GB59 | 2620,30 | 13,00 | 10,34 | 2,66 | 7,0756 |
| GB60 | 3,11 | 0,00 | 3,67 | -3,67 | 13,4689 |
Kamu dapat menghitung jumlah kuadratnya dengan menjumlahkan semua nilai dalam kolom Kuadrat Galat. Hasilnya, SSE = 1315,3433.
Untuk menentukan akar dari rerata kuadrat galatnya (RMSE), kamu terlebih dahulu hitung rerata semua nilai dalam kolom Kuadrat Galat, kemudian akarkuadratkan hasilnya. Dengan demikian, hasilnya adalah RMSE ≈ 4,6821.
Kamu juga dapat menghitung SSE dan RMSE dari model fungsi rasional dengan menggunakan cara yang serupa. Untuk model ini, hasilnya adalah SSE = 212,6785 dan RMSE ≈ 1,8827.
Kamu dapat menyajikan SSE dan RMSE untuk model linear dan rasional tersebut seperti pada Tabel 2 berikut.
| Model | SSE | RMSE |
|---|---|---|
| Fungsi linear | 1315,3433 | 4,6821 |
| Fungsi rasional | 212,6785 | 1,8827 |
Model manakah yang lebih baik? Karena SSE fungsi rasional kurang dari SSE fungsi linear, fungsi rasionallah yang lebih baik. (Dalam membandingkan model, kamu dapat memilih salah satu dari SSE dan RMSE untuk dibandingkan nilainya.)
Catatan Akhir
Kamu telah melihat bagaimana berharganya matematika. Matematika dapat digunakan untuk memodelkan keanekaragaman hayati di Kepulauan Raja Ampat dan menilai seberapa baik modelnya. Dalam menilai model matematika, kamu dapat menggunakan cara visual dengan mengamati visualisasi data dan modelnya. Selain itu, kamu dapat memanfaatkan galat untuk menilai model tersebut. Ketika menggunakan galat, kamu dapat menggunakan salah satu dari SSE atau RMSE. Model yang lebih baik memiliki SSE (atau RMSE) yang lebih kecil.
Apa selanjutnya? Apabila kamu tertarik dengan pemodelan matematika, kamu dapat berlatih melakukan pemodelan dengan fungsi-fungsi lainnya. Misalnya, kamu dapat mengunjungi aplikasi Pemodelan Fungsi Polinomial untuk memodelkan masalah-masalah pada bidang pangan, pariwisata, ekonomi, dan musik dengan menggunakan fungsi polinomial.
Gambar sampul artikel ini bersumber dari Julian Schrader / julianschrader.wordpress.com.
Kristanto Math 