Bagaimana membuat pembelajaran Matematika pada topik kekongruenan menjadi dinamis? Tulisan ini memberikan pandangan bahwa kekongruenan bangun datar perlu dikenalkan dengan menggunakan transformasi geometri. Lebih jauh, konsekuensinya mengenai desain pembelajaran dan implementasinya juga diilustrasikan dan dijelaskan secara ringkas.
Matematika seharusnya tidak diberikan kepada peserta didik, melainkan sebaliknya. Peserta didiklah yang secara aktif perlu menemukan, melakukan, dan berpikir tentang matematika. Proposisi tersebut tentu juga berlaku untuk topik kekongruenan. Untuk melakukannya, kekongruenan tersebut perlu dibuat dinamis agar peserta didik terlibat aktif, baik secara fisik maupun kognitif.
Matematika seharusnya tidak diberikan kepada peserta didik, melainkan sebaliknya. Peserta didiklah yang secara aktif perlu menemukan, melakukan, dan berpikir tentang matematika.
Dinamis erat kaitannya dengan gerakan, penuh semangat, dan berenergi. Bagaimana membuat topik kekongruenan menjadi seperti ini? Jawabannya adalah dengan menggunakan transformasi geometri, khususnya isometri. Isometri yang dasar terdiri dari tiga jenis transformasi: translasi, refleksi, dan rotasi.
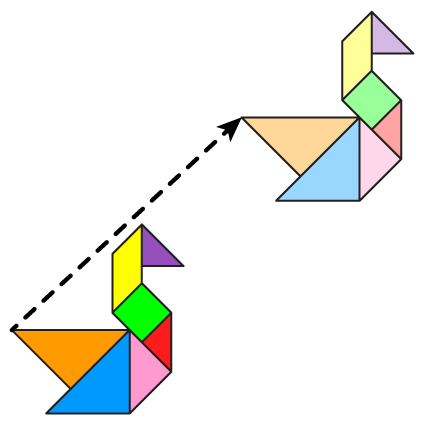
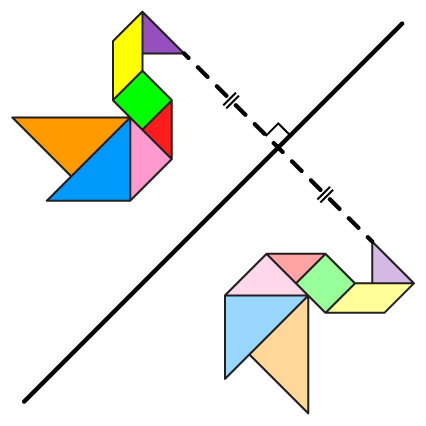
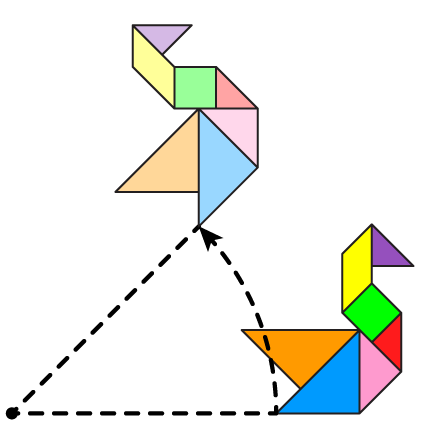
Istilah isometri berasal dari bahasa Yunani kuno, yaitu isos yang berarti “sama” dan metron yang memiliki makna “ukuran”. Seperti namanya, salah satu sifat isometri adalah mempertahankan ukuran, baik jarak maupun besar sudut. Selain itu, isometri memetakan garis ke garis, sinar garis ke sinar garis, dan ruas garis ke ruas garis.
Penggunaan kata “memetakan” dalam menyebutkan sifat isometri pada paragraf sebelumnya merujuk pada fakta bahwa isometri, atau transformasi secara umum, merupakan fungsi. Akan tetapi, agar membuat matematika menjadi dinamis, konsep pemetaan tersebut selanjutnya kita ganti dengan pemindahan. Misalnya, daripada mengatakan sebuah translasi T memetakan titik A ke T(A), kita nyatakan translasi T tersebut memindahkan titik A ke T(A). Selain dinamis, cara seperti ini tidak hanya memfokuskan transformasi pada objek asal dan hasilnya, tetapi juga pada prosesnya. Dengan demikian, transformasi menjadi lebih intuitif.
Definisi Kekongruenan pada Bangun Datar
Secara intuitif, dua bangun datar dikatakan kongruen jika keduanya memiliki bentuk dan ukuran yang sama. Bagaimana kita dapat menilai dua bangun datar tersebut memiliki bentuk dan ukuran yang sama? Mungkin kita berpikir seperti ini, “Jika bangun datar pertama ditumpangkan dan berimpit ke bangun datar kedua, kedua bangun tersebut sama bentuk dan ukurannya”.
Proses menumpangkan bangun datar pertama ke bangun datar kedua tersebut dapat melibatkan pergeseran, pembalikan, atau pemutaran. Dengan demikian, kekekongruenan dua bangun datar dapat didefinisikan secara lebih presisi seperti berikut.
| Definisi Kekongruenan Dua bangun datar kongruen jika dan hanya jika terdapat isometri tunggal atau komposisi isometri yang memindah bangun datar pertama sehingga berimpit dengan bangun datar kedua. |
Sekarang Anda bayangkan bagaimana dinamisnya peserta didik ketika menunjukkan kekongruenan dua bangun datar dengan menggunakan definisi tersebut. Mereka memotong. Mereka menggeser, membalik, atau memutar potongan tersebut ke bangun datar yang lain. Mereka kemudian memutuskan apakah keduanya kongruen.
Mereka mungkin memakai mika bening. Mereka jiplak bangun datar pertama pada mika tersebut. Mereka atur mikanya untuk mengetahui apakah jiplakan tersebut dapat berimpit dengan bangun datar kedua.
Bagaimana potensi teknologi dalam pembuktian kekongruenan dua bangun datar? Potensi teknologi tentu lebih besar daripada sebelumnya. Perangkat lunak geometri dinamis, seperti GeoGebra, Desmos, dan Cabri Express, dapat digunakan peserta didik sebagai alat untuk mengutak-atik objek geometris. Mereka dapat melakukan translasi, refleksi, maupun rotasi terhadap objek tersebut secara interaktif. Kedinamisan geometri yang ditawarkan perangkat lunak semacam ini sangat mendukung pembuktian kekongruenan dengan menggunakan isometri.
Pendefinisian kekongruenan yang menggunakan isometri tidak secara ekslusif diperuntukkan bagi segi-segi banyak. Hal ini berbeda dengan definisi tradisional yang tergantung pada kesamaan panjang sisi dan besar sudut. Dengan menggunakan isometri, peserta didik dapat menyelidiki kekongruenan bangun-bangun datar selain segi banyak, misalnya elips. Dengan demikian, definisi tersebut dapat digunakan secara lebih luas.
Ringkasnya, banyak peluang yang ditemukan dalam topik kekongruenan ketika topik tersebut didefinisikan dengan menggunakan isometri. Menyadari peluang tersebut, beberapa negara secara jelas memandatkan agar kekongruenan dikenalkan dari transformasi geometri. Negara-negara tersebut misalnya Amerika Serikat dan Australia. Di dalam standar mata pelajaran Matematika di Amerika Serikat, salah satu capaian pembelajarannya berbunyi, “understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them”. Salah satu capaian pembelajaran di Australia juga kurang lebih sama, “define congruence of plane shapes using transformations”. Hal ini menunjukkan bahwa pengenalan kekongruenan dari transformasi geometri secara luas telah digunakan di dalam pembelajaran matematika.
Apa Konsekuensinya?
Di dalam buku Matematika untuk SMP/MTs Kelas IX, kami memanfaatkan kedinamisan transformasi geometri untuk memperkenalkan konsep kekongruenan bangun datar. Pilihan ini tentu memberikan dampak terhadap wajah dan progres matematika yang diterima oleh peserta didik dalam penuntasan capaian pembelajaran fase D tentang kekongruenan. Capaian pembelajaran tersebut menuntut peserta didik untuk “… dapat menjelaskan sifat-sifat kekongruenan … pada segitiga dan segi empat, dan menggunakannya untuk menyelesaikan masalah”.
Capaian pembelajaran itulah yang menjadi destinasi peserta didik di topik kekongruenan. Setelah destinasi ditentukan, tidak kalah penting untuk menentukan bagaimana perjalanannya. Perjalanan tersebut perlu memberikan pengalaman yang berkesan dan bermakna bagi peserta didik. Berikut ini adalah contoh alur tujuan pembelajaran yang dapat ditempuh peserta didik untuk mencapai destinasinya.
TP 1: Peserta didik memahami karakteristik isometri (translasi, refleksi, dan rotasi) berdasarkan bentuk dan ukurannya
Modal utama untuk mendefinisikan kekonguenan adalah karakteristik isometri. Oleh karena itu, penting untuk memastikan bahwa peserta didik memahami betul karakteristik tersebut. Hal ini dapat dilakukan dengan mengajak peserta didik untuk mengamati sebuah objek geometris dan bayangannya setelah objek tersebut dikenakan translasi, rotasi, refleksi, dan komposisi isometri tersebut. Pengamatan tersebut diharapkan dapat memantik peserta didik untuk menyimpulkan bahwa jika sebuah objek geometris dikenakan isometri tunggal atau komposisinya, objek tersebut memiliki bentuk dan ukuran yang sama dengan bayangannya.
Untuk memperkaya pengalaman peserta didik, mereka juga dapat diajak untuk menyelidiki konvers dari kesimpulan sebelumnya. Untuk melakukannya, mereka dapat diberikan dua pasang bangun datar. Pasangan pertama memiliki bentuk dan ukuran yang sama, sedangkan pasangan kedua tidak memiliki bentuk dan ukuran yang sama. Selanjutnya, mereka diminta untuk menyelidiki apakah ada isometri tunggal atau komposisinya yang dapat memindah bangun datar pertama agar berimpit dengan bangun datar kedua di tiap pasangan. Selain memperkaya pengalaman peserta didik, aktivitas seperti ini akan membuat mereka memahami bahwa hubungan antara isometri dan kekongruenan adalah hubungan dua arah.
TP 2: Menjelaskan pengertian kekongruenan berdasarkan karakteristik isometri (translasi, refleksi, dan rotasi)
Di tahap ini, peserta didik memperluas kosakata atau perbendaharaan katanya. Mereka untuk pertama kalinya mengenal kata “kongruen”, yang di dalam KBBI dikategorikan ke dalam n Mat. Artinya, kata itu merupakan kata spesifik yang ada di dalam bidang matematika. Dengan demikian, di tahap ini peserta didik mengembangkan literasinya dengan memahami kata kongruen dan kekongruenan berdasarkan pengalaman yang mereka alami sebelumnya.
Tahapan ini dapat dilakukan dengan mengenalkan secara langsung istilah kongruen kepada peserta didik. Misalnya, guru dapat menerangkan, “Anak-anak, kalian beberapa kali sudah mengamati dua bangun datar yang bentuk dan ukurannya sama. Di dalam matematika kedua bangun datar tersebut dikatakan kongruen”. Pengenalan ini selanjutnya perlu diikuti dengan pendefinisian kekongruenan secara lebih presisi. Proses pendefinisian ini sebaiknya melibatkan pemikiran matematis peserta didik. Berikut ini adalah contoh bagaimana guru mengundang, merayakan, dan menggunakan pemikiran peserta didik untuk membuat kesepakatan tentang definisi kekongruenan.
| Guru: | Anak-anak, menurut kalian, bagaimana kita tahu bahwa dua bangun datar itu kongruen? |
| Amir: | [Amir angkat tangan.] Menurut saya, kedua bangun datar tersebut sama bentuk dan ukurannya, Bu. |
| Guru: | Bagus! Citra, bisakah kamu lebih memperjelas pendapatnya Amir? Bagaimana cara kita tahu bahwa dua bangun datar itu memiliki bentuk dan ukuran yang sama? |
| Citra: | Emm … [Citra diam sejenak.] Kita dapat mengukur bagian-bagian dari kedua bangun datar tersebut, Bu. |
| Guru: | Mantap! Untuk semuanya, apakah ada cara lain? Bagaimana cara kita mengetahui apakah dua bangun datar itu kongruen? [Setelah mengetahui semua peserta didik terdiam, guru mengambil dua buku catatan yang bentuk dan ukurannya sama.] Anak-anak, bagaimana cara kalian meyakinkan saya bahwa sampul kedua buku ini kongruen? Ayo siapa yang ingin mencoba, maju ke depan! [Guru kemudian meletakkan kedua buku itu di meja.] |
| Martha: | [Martha maju ke depan. Dia kemudian meletakkan satu buku di atas buku lainnya sehingga kedua buku tersebut tepat berimpit.] Begini, Bu. Kedua buku ini pas. |
| Guru: | Hebat! Begini yang dilakukan oleh Martha tadi, anak-anak. [Guru mengulangi apa yang dilakukan oleh Martha, tetapi dengan membuat agar proses translasi dan rotasi bukunya tampak jelas kepada semua peserta didik.] Martha tadi mentranslasi buku ini, kemudian merotasikannya sehingga buku ini berada di atas dan berimpit dengan buku yang kedua. [Guru jeda sejenak.] Kemudian, Martha menyimpulkan bahwa sampul kedua buku ini kongruen. [Guru jeda sejenak.] Adakah yang bisa menyatakan ulang cara Martha tadi, anak-anak? |
| Amir: | [Amir angkat tangan.] Martha menggunakan translasi dan rotasi agar buku pertama bisa pas di atas buku yang kedua, Bu. |
| Guru: | Nah, caranya Martha tadi dapat kita gunakan untuk membuat definisi tentang kekongruenan bangun datar. Meskipun Martha tadi tidak menggunakan refleksi, kita dapat juga menggunakan refleksi. [Guru mendemonstrasikan penggunaan refleksi dengan membalik buku menurut suatu garis, yaitu salah satu tepian buku.] Dengan demikian, kita dapat menyimpulkan bahwa dua bangun datar dikatakan kongruen jika terdapat transformasi kaku tunggal, yaitu translasi, refleksi, atau rotasi, atau rangkaian transformasi kaku yang membuat bangun datar pertama tepat berimpit dengan bangun datar kedua. [Guru kemudian menuliskan apa yang dinyatakan tersebut ke papan tulis.] |
Strategi yang dilakukan oleh guru dalam mengajak peserta didik mendefinisikan kekongruenan tersebut bersumber dari pemikiran peserta didik. Hal ini penting agar peserta didik merasa didengar. Selain itu, ketika definisi tersebut dibuat seolah-olah berasal dari peserta didik sendiri, mereka akan lebih dekat dan terhubung dengan definisi tersebut. Akibatnya, mereka akan memiliki pemahaman yang kuat terhadap konsep kekongruenan bangun datar.
TP 3: Menganalisis karakteristik kekongruenan pada segi banyak
Pencapaian tujuan pembelajaran ini diawali dengan pengenalan istilah-istilah penting, yaitu sisi-sisi dan sudut-sudut yang bersesuaian. Istilah-istilah tersebut penting bagi peserta didik untuk menyelidiki dan memahami sifat-sifat kekongruenan pada segi banyak. Dengan demikian, literasi peserta didik berkembang di sini.
Setelah peserta didik memahami sisi-sisi dan sudut-sudut yang bersesuaian, mereka dapat diajak untuk menyelidiki karakteristik kekongruenan pada segi banyak. Untuk melakukannya, mereka mengamati dua segi banyak, segi lima misalnya, yang kongruen. Mereka diminta untuk mengukur panjang setiap sisi dan besar sudut yang bersesuaian dari kedua segi lima tersebut. Setelah itu mereka diminta untuk menunjukkan apakah ada isometri yang membuat segi lima pertama berimpit dengan segi lima kedua. Aktivitas seperti ini diharapkan dapat menggiring peserta didik untuk menyimpulkan bahwa dua segi banyak dikatakan kongruen jika (a) sisi-sisi yang bersesuaiannya sama panjang, dan (b) sudut-sudut yang bersesuaiannya sama besar.
Kesimpulan itulah yang biasanya menjadi definisi kekongruenan pada bangun-bangun datar. Dengan pendekatan transformasi, pernyataan itu tidak lagi menjadi definisi melainkan menjadi sifat. Hal ini tentu memberikan ruang yang lebih besar bagi peserta didik untuk bermatematika.
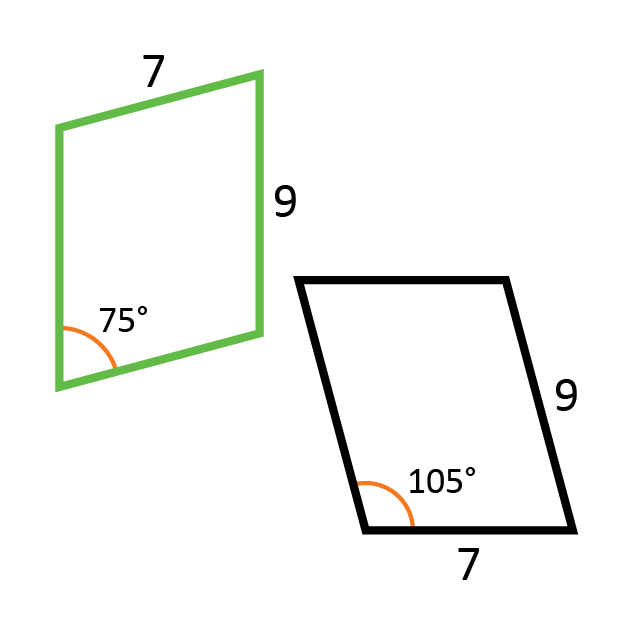
Penemuan karakteristik kekongruenan pada segi banyak tersebut tentu memberikan dampak terhadap perjalanan peserta didik selanjutnya. Mereka tidak lagi wajib memanfaatkan isometri untuk menunjukkan kekongruenan dua segi banyak. Alih-alih, mereka dapat melakukan deduksi dari pengetahuan mereka sebelumnya tentang sifat-sifat segi banyak untuk menunjukkan bahwa sisi-sisi dan sudut-sudut yang bersesuaian dari dua segi banyak yang mereka selidiki memiliki ukuran yang sama atau kongruen. Sebagai contoh, untuk membuktikan bahwa dua jajar genjang di samping kongruen, mereka dapat langsung menggunakan sifat-sifat jajar genjang. Sifat-sifat tersebut digunakan untuk mendeduksi bahwa kedua jajar genjang tersebut sisi-sisi dan sudut-sudut yang bersesuaiannya kongruen.
TP 4: Menganalisis karakteristik kekongruenan pada segitiga
Tujuan akhir di tahap ini adalah agar peserta didik mampu menganalisis karakteristik kekongruenan pada segitiga. Hal ini ditujukan kepada pemahaman tentang tiga kriteria kekongruenan pada segitiga, yaitu sudut-sisi-sudut (sd.s.sd), sisi-sudut-sisi (s.sd.s), dan sisi-sisi-sisi (s.s.s).
Di dalam buku Matematika untuk SMP/MTs Kelas IX, kami mengajak peserta didik untuk melakukan penyelidikian yang taktil dan kinetik. Melalui penyelidikan tersebut, peserta didik diajak untuk menemukan kriteria sudut-sisi-sudut secara induktif dengan menggunakan ide transformasi geometri. Runtutan persoalan yang kami pilih untuk mencapai tujuan tersebut dipaparkan di bawah ini.
Soal 1: Pada selembar kertas, lukislah sebuah segitiga yang besar dua sudut dalamnya adalah 60° dan 75°, serta panjang sisi di antara kedua sudut tersebut adalah 25 cm.
Soal 2: Guntinglah segitiga yang telah kalian lukis dan tukarkan segitiga tersebut dengan segitiga yang diperoleh teman kalian! (Sebelum ditukar, sebaiknya kalian mencantumkan nama kalian di segitiga yang kalian buat.)
Soal 3: Koreksilah potongan segitiga milik teman kalian apakah besar dua sudutnya 60° dan 75°, serta panjang sisi yang diapit kedua sudut tersebut adalah 25 cm. Jika belum sesuai, bantulah teman kalian untuk membuat segitiga yang sesuai dengan informasi yang diberikan!
Soal 4: Bandingkan segitiga kalian dengan segitiga milik teman-teman kalian. Apa yang dapat kalian simpulkan?
Melalui aktivitas penyelidikan tersebut, tentu peserta didik diharapkan untuk mencapai tujuan yang ditetapkan. Tujuannya adalah menemukan dan memahami kriteria kekongruenan sudut-sisi-sudut (sd.s.sd). Meskipun demikian, aktivitas tersebut tidak semata-mata dimaksudkan untuk mencapai destinasi tersebut. Lebih dari itu, aktivitas tersebut dimaksudkan agar peserta didik mengenali wajah sosial dari matematika. Matematika bukan semata-mata aktivitas individu. Ketika bermatematika, mereka ternyata dapat membangun pengetahuan secara kolektif melalui pertukaran karya dan gagasan dengan teman-temannya.
Aktivitas penyelidikan yang telah didiskusikan sebelumnya memang hanya ditujukan untuk menemukan dan memahami kriteria sudut-sisi-sudut. Hal ini dimaksudkan agar peserta didik menggunakan pemahaman tersebut untuk mempelajari dua kriteria lainnya, yaitu sisi-sudut-sisi dan sisi-sisi-sisi.
Catatan Penutup
Tulisan ini telah memberikan argumen bahwa peserta didik perlu menjadi aktor utama dalam petualangannya untuk mempelajari topik kekongruenan. Agar selama petualangan tersebut peserta didik penuh semangat dan energik, wajah topik kekongruenan perlu dibuat dinamis. Untuk itu, kami menawarkan pendekatan yang berbeda di dalam buku Matematika untuk SMP/MTs Kelas IX. Di buku itu, kami mengajak peserta didik untuk menggunakan transformasi geometri dalam memahami topik kekongruenan bangun datar. Pendekatan ini memberikan ruang yang lebih luas bagi mereka untuk bermatematika secara taktil dan kinetik. Selain itu, pendekatan tersebut juga memperluas wawasan mereka bahwa kekongruenan itu tidak secara eksklusif untuk segi banyak, tetapi untuk bangun-bangun datar lainnya.
Tulisan ini juga telah memberikan contoh dan ilustrasi bagaimana seharusnya peserta didik berjumpa dengan matematika. Di dalam pembelajaran matematika, pemikiran peserta didik perlu diundang, digunakan, dan bahkan dirayakan. Cara seperti ini diharapkan agar membuat peserta didik merasa memiliki terhadap matematika yang mereka pelajari.
Di dalam pembelajaran matematika, pemikiran peserta didik perlu diundang, digunakan, dan bahkan dirayakan.
Selain itu, pembelajaran matematika juga perlu memberikan ruang bagi peserta didik untuk berinteraksi dan berbagi karya maupun gagasan kepada teman-teman dan gurunya. Wajah sosial matematika ini diharapkan menumbuhkembangkan persepsi positif peserta didik tentang matematika. Mereka tidak lagi membayangkan matematika sebagai kegiatan pengerjaan soal yang dilakukan secara individu dan dilakukan di dalam kamar yang terkunci rapat-rapat. Akan tetapi, mereka akan memandang matematika sebagai sebuah mata pelajaran yang membutuhkan suasana kolaborasi dan gotong royong dalam mencapai destinasi bersama.
Apa selanjutnya? Potensi matematika dinamis yang dipaparkan dalam artikel ini masih dapat dikembangkan ke topik-topik lainnya, khususnya kesebangunan. Dengan menambahkan dilatasi, kita dapat memaknai kesebangunan dari perspektif transformasi geometri. Topik kesebangunan yang dinamis juga memberikan peluang terciptanya pembelajaran yang aktif dan energik, serta taktil, kinetik, dan kolaboratif.
Artikel ini dimaksudkan sebagai pendamping Buku Panduan Guru Matematika untuk SMP/MTs Kelas IX, buku yang diterbitkan oleh Pusat Perbukuan, Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi. Pandangan dan pendapat yang diberikan dalam artikel ini merupakan pandangan dan pendapat penulis. Pandangan dan pendapat tersebut tidak merefleksikan pandangan dan pendapat Pusat Perbukuan maupun Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi.
Gambar sampul di awal artikel ini diperoleh dari karya yang berjudul “The Beauty of Dynamic Mathematics” di kalkulator grafik Desmos.
Ingin membaca lagi artikel ini secara luring atau mencetaknya? Silakan unduh artikel ini dalam versi PDF.